Статистическая ошибка среднего - это предельная величина ошибки, которая возникает при оценке среднего арифметического большого числа независимых и одинаково распределенных чисел. Вероятность возникновения такой ошибки описывается теоремой центральной предельной, которая является одной из основных теорем в математической статистике.
Суть центральной предельной теоремы заключается в том, что сумма большого числа независимых и одинаково распределенных случайных величин приближается к нормальному распределению. Именно поэтому ошибка среднего возникает при работе с большими числами - когда мы применяем среднее арифметическое к большому количеству чисел, оно начинает приближаться к нормальному распределению.
Как избежать ошибки среднего? Один из способов - увеличить количество наблюдений. Чем больше независимых и одинаково распределенных чисел мы имеем, тем точнее будет наше среднее значение. Также важно учесть, что ошибка среднего может быть снижена при использовании других методов оценки среднего, например, медианного.
В любом случае, важно помнить о наличии статистической ошибки среднего и учитывать ее при анализе данных. Это поможет сделать более точные выводы и принять обоснованные решения на основе статистических данных.
В итоге, ошибка среднего - это статистическая ошибка, которая возникает при оценке среднего арифметического большого числа независимых и одинаково распределенных чисел. Она описывается теоремой центральной предельной и может быть уменьшена при увеличении количества наблюдений и использовании других методов оценки. Важно помнить об этой ошибке при работе с данными и учесть ее при анализе и принятии решений на основе статистических данных.
Ошибка среднего: что это такое и как избежать?
Центральная предельная теорема
Одним из способов избежать ошибки среднего является применение центральной предельной теоремы. Эта теорема гласит, что сумма большого числа независимых и одинаково распределенных случайных величин будет асимптотически нормально распределена. То есть, что даже если исходные данные имеют не нормальное распределение, сумма большого числа таких данных будет все равно иметь распределение, близкое к нормальному. Это позволяет использовать статистические методы, основанные на нормальном распределении, для анализа среднего значения.
Использование больших выборок
Еще один способ избежать ошибку среднего – использовать большие выборки. Чем больше наблюдений мы включаем в анализ, тем более точные результаты мы получаем. Большие выборки позволяют учесть большее количество случайных факторов и уменьшают влияние случайных отклонений. Таким образом, использование больших выборок помогает минимизировать ошибку среднего и получить более надежные статистические результаты.
Программы ошибок и как их исправить
Центральная предельная теорема
Центральная предельная теорема – это одна из основных теорем математической статистики, которая позволяет объяснить, почему среднее значение выборки стремится к нормальному распределению даже в том случае, если исходная генеральная совокупность не имеет нормального распределения. Она устанавливает, что при достаточно большом числе независимых и одинаково распределенных случайных величин их сумма аппроксимируется нормальным распределением.
Закон статистической больших чисел
Закон статистической больших чисел – это теорема, утверждающая, что при повторном независимом проведении случайного эксперимента среднее арифметическое значений случайной величины сходится почти наверное к ее математическому ожиданию. Иными словами, с увеличением числа экспериментов среднее значение выборки приближается к истинному среднему значению генеральной совокупности.
Ошибки, связанные с неграмотным применением центральной предельной теоремы или закона статистической больших чисел, могут привести к искажению результатов статистического анализа и ошибочным выводам. Для избежания таких ошибок необходимо тщательно изучить эти теоремы и применять их правильно при анализе данных.
Как избежать ошибок при подсчете среднего значения
Закон больших чисел
Закон больших чисел – это математический закон, согласно которому с увеличением числа испытаний среднее значение результатов этих испытаний приближается к математическому ожиданию. Используя этот закон, можно повысить точность расчетов среднего значения.
Центральная предельная теорема
Центральная предельная теорема утверждает, что сумма большого числа случайных величин с абсолютно любым распределением будет приближаться к нормальному распределению. Применение этой теоремы позволяет сократить возможные ошибки при подсчете среднего значения.
Таким образом, применение статистических законов и теорем может помочь избежать ошибок при подсчете среднего значения. Это особенно важно при работе с большими числами, где даже небольшая ошибка может привести к значительным искажениям результатов анализа данных.
Закон больших чисел
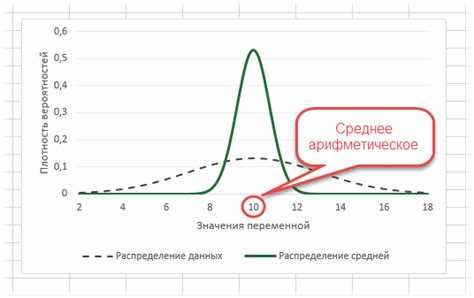
Предельная форма закона больших чисел позволяет сделать вывод о том, что с увеличением объёма выборки среднее арифметическое приближается к математическому ожиданию. Это означает, что величина ошибки среднего уменьшается с ростом объёма выборки, что является важным результатом для применения статистических методов.
Центральная статистическая теорема
Центральная статистическая теорема является обобщением закона больших чисел. Она утверждает, что сумма большого числа независимых и одинаково распределенных случайных величин имеет приближенно нормальное распределение. Таким образом, величины ошибок среднего можно описать с помощью нормального распределения.
Закон больших чисел
Таким образом, закон больших чисел и центральная статистическая теорема являются важными результатами в теории вероятностей и статистике. Они дают возможность делать выводы о поведении случайных величин и оценивать ошибку при использовании среднего.
Определение и применение закона больших чисел
Центральная предельная теорема и статистическая теорема о законе средних чисел являются основополагающими для закона больших чисел.
Центральная предельная теорема утверждает, что сумма большого количества независимых, одинаково распределенных случайных величин имеет распределение, которое стремится к нормальному приближению, независимо от формы их исходных распределений.
Статистическая теорема о законе средних чисел объясняет, что среднее значение последовательности независимых случайных величин сходится к математическому ожиданию этой последовательности при условии, что размер выборки достаточно большой.
Закон больших чисел даёт нам соответствующие статистические инструменты для оценки и предсказания средних значений в случайных выборках путем использования большого количества данных. Это позволяет избежать ошибки, возникающей из-за небольшой выборки и увеличить точность и достоверность наших выводов и прогнозов.
Использование закона больших чисел в статистике
Важно отметить, что при работе с выборкой невозможно избежать ошибки. Одной из наиболее распространенных ошибок является ошибка среднего, когда выборочное среднее отклоняется от истинного среднего. Здесь на помощь приходит теорема о законе больших чисел.
Теорема о законе больших чисел
Теорема о законе больших чисел утверждает, что при увеличении размера выборки, выборочное среднее стремится к истинному среднему значению всей группы данных. Таким образом, ошибка среднего снижается с увеличением размера выборки.
Применение теоремы о законе больших чисел в статистике позволяет нам делать выводы о генеральной совокупности на основе выборочных данных. С помощью этой теоремы мы можем избежать субъективных ошибок и делать более точные статистические выводы.
Центральная предельная теорема
Центральная предельная теорема - это другая важная теорема в статистике, которая утверждает, что сумма независимых и одинаково распределенных случайных величин приближается к нормальному распределению с увеличением размера выборки. Это позволяет нам использовать нормальное распределение для оценки вероятности того, что среднее значение попадет в определенный диапазон.
Использование центральной предельной теоремы помогает избежать ошибок, связанных с оценкой вероятностей на малых выборках, и позволяет применять статистические методы в широком диапазоне ситуаций.
Центральная предельная теорема
Статистическая ошибка
Статистическая ошибка – это разница между оценкой и истинным значением показателя, которую можно объяснить только случайностью выборки. Влияние случайности выборки может проявляться во всех виде исследований, включая эксперименты, наблюдения и опросы. Ошибка среднего является одним из видов статистической ошибки.
Предельная центральная теорема
Предельная центральная теорема, также известная как закон больших чисел, утверждает, что сумма большого числа некоррелированных случайных величин с конечными средними будет приближаться к нормальному распределению. Это означает, что даже если исходные данные не имеют нормального распределения, с ростом объема выборки среднее значение выборки будет стремиться к нормальному распределению.
Основные принципы и результаты центральной предельной теоремы
Статистическая предельная теорема
Статистическая предельная теорема утверждает, что при определенных условиях сумма большого числа независимых случайных величин стремится к нормальному распределению. Это означает, что при увеличении числа слагаемых в сумме, ошибка аппроксимации среднего значения этой суммы нормальным распределением уменьшается.
Центральная предельная теорема
Центральная предельная теорема, относящаяся к средним значениям, утверждает, что сумма большого числа независимых случайных величин будет распределена нормально, независимо от распределений исходных случайных величин. Это означает, что при достаточно большом числе слагаемых ошибка аппроксимации среднего значения этой суммы нормальным распределением будет мала.
| Теорема | Результат |
|---|---|
| Статистическая предельная теорема | При увеличении числа слагаемых в сумме, ошибка аппроксимации среднего значения этой суммы нормальным распределением уменьшается. |
| Центральная предельная теорема | При достаточно большом числе слагаемых ошибка аппроксимации среднего значения этой суммы нормальным распределением будет мала. |
Применение центральной предельной теоремы в практике и исследованиях
В практике и исследованиях центральная предельная теорема позволяет использовать нормальное распределение в случаях, когда распределение исследуемой статистической величины неизвестно или не имеет нормальную форму. Это особенно полезно при работе с большими объемами данных, когда использование других методов может быть затруднено.
Применение центральной предельной теоремы позволяет проводить статистический анализ и сделать выводы, основываясь на средних значений и суммах случайных величин. Ошибка среднего, или ошибка, связанная с оценкой среднего значения исследуемой величины, может быть минимизирована с помощью центральной предельной теоремы.
Статистическая ошибка
Центральная предельная теорема является основой для закона больших чисел. Закон больших чисел утверждает, что с ростом числа наблюдений среднее значение выборки будет ближе к среднему значению генеральной совокупности. Однако, если величина выборки слишком мала, то предположения центральной предельной теоремы могут нарушиться, что приводит к статистической ошибке.
Статистическая ошибка может быть уменьшена путем увеличения размера выборки. Чем больше числа в выборке, тем более точной будет оценка среднего значения. Также можно использовать более сложные методы статистического анализа, такие как коррекция на скошенность или нелинейное преобразование данных, чтобы уменьшить статистическую ошибку.
Итак, статистическая ошибка, или ошибка среднего, является результатом применения центральной предельной теоремы и закона больших чисел к выборкам недостаточно большого размера. Для избежания статистической ошибки, необходимо знать и использовать правильные методы статистического анализа и увеличивать размеры выборки.
Видео:
Как женщине изменить свою жизнь к лучшему всего за 1 год
Как женщине изменить свою жизнь к лучшему всего за 1 год by Марк Бартон 650,185 views 5 months ago 29 minutes
Вопрос-ответ:
Что такое ошибка среднего?
Ошибка среднего - это концепция, связанная с измерением и обработкой данных. Она указывает на разницу между средним значением выборки и истинным средним значением всей генеральной совокупности. Ошибка среднего может возникнуть из-за случайной выборки или систематической ошибки в измерениях. Чтобы избежать ошибки среднего, необходимо учитывать стандартное отклонение и размер выборки при интерпретации среднего значения.
Что такое закон больших чисел?
Закон больших чисел - это концепция, которая утверждает, что с увеличением размера выборки среднее значение выборки всегда будет стремиться к истинному среднему значению генеральной совокупности. Это означает, что с увеличением размера выборки статистические выводы становятся более надежными. Закон больших чисел является одним из основных принципов статистики и широко используется в исследованиях и анализе данных.
Что такое центральная предельная теорема?
Центральная предельная теорема - это фундаментальный результат в вероятностной теории и статистике. Она гласит, что сумма или среднее большого количества независимых и одинаково распределенных случайных величин стремится к нормальному распределению, даже если исходные величины не имеют нормального распределения. Эта теорема имеет огромное практическое значение, так как многие статистические тесты и методы основываются на ней. Она также объясняет, почему нормальное распределение встречается так часто в естественных и социальных науках.