Коэффициент множественной корреляции является одним из наиболее популярных и мощных инструментов в статистике. Он позволяет измерить степень связи между несколькими переменными и предсказать значения одной переменной на основе других. Таким образом, коэффициент множественной корреляции позволяет исследователям понять, какие факторы влияют на зависимую переменную и в какой степени.
Корреляция - это мера степени взаимосвязи между двумя переменными. Коэффициент множественной корреляции, или R-квадрат, это мера степени детерминации, то есть объяснения зависимой переменной с помощью независимых переменных. Он может принимать значения от 0 до 1, где 0 означает отсутствие связи, а 1 - идеальную связь.
Для расчета коэффициента множественной корреляции необходимо иметь данные по зависимой переменной и независимым переменным. Часто, для более точного анализа, используется несколько независимых переменных. Существует несколько методов расчета коэффициента множественной корреляции, включая метод наименьших квадратов и метод множественной регрессии.
Что такое коэффициент множественной корреляции и как его рассчитать?
Коэффициент множественной корреляции обозначается символом R или R-квадрат (R^2). Значение коэффициента множественной корреляции может быть от 0 до 1. Чем ближе значение к 1, тем сильнее взаимосвязь между переменными. Значение близкое к 0 указывает на отсутствие связи или слабую связь между переменными.
Чтобы рассчитать коэффициент множественной корреляции, необходимо использовать специальные статистические методы. Один из наиболее распространенных способов рассчета заключается в использовании множественной регрессионной анализа. В этом методе зависимая переменная связывается с набором независимых переменных, и рассчитывается коэффициент детерминации.
Коэффициент детерминации, обозначенный как R^2, представляет собой процент изменчивости зависимой переменной, который может быть объяснен моделью множественной регрессии. Высокое значение R^2 указывает, что модель хорошо объясняет изменчивость зависимой переменной, тогда как низкое значение R^2 может означать, что модель плохо описывает данные.
В заключение, коэффициент множественной корреляции является важной статистической мерой, которая помогает определить степень связи между переменными в множественном регрессионном анализе. Расчет этого коэффициента позволяет оценить влияние независимых переменных на зависимую переменную и понять, насколько хорошо модель регрессии объясняет данные.
Множественная корреляция: определение и сущность концепции
Коэффициент множественной корреляции является мерой множественной корреляции и обозначается как R. Он может принимать значения от -1 до 1, где -1 указывает на обратную связь, 0 - на отсутствие связи, а 1 - на положительную связь. Коэффициент множественной корреляции показывает силу и направление связи между независимыми и зависимой переменными.
Сущность множественной корреляции
Корреляция является инструментом, который позволяет нам измерить степень взаимосвязи между переменными. Оперируя понятием корреляции, множественная корреляция учитывает несколько независимых переменных, что позволяет получить более полную картину взаимосвязи между переменными в сравнении с простой корреляцией.
Коэффициент множественной корреляции показывает долю дисперсии зависимой переменной, которая может быть объяснена значениями независимых переменных в модели множественной регрессии. Иными словами, он позволяет определить, насколько хорошо модель может предсказывать значения зависимой переменной.
Пример расчета коэффициента множественной корреляции
| Зависимая переменная | Независимая переменная 1 | Независимая переменная 2 |
|---|---|---|
| Y | X1 | X2 |
| 10 | 3 | 5 |
| 15 | 5 | 7 |
| 20 | 7 | 9 |
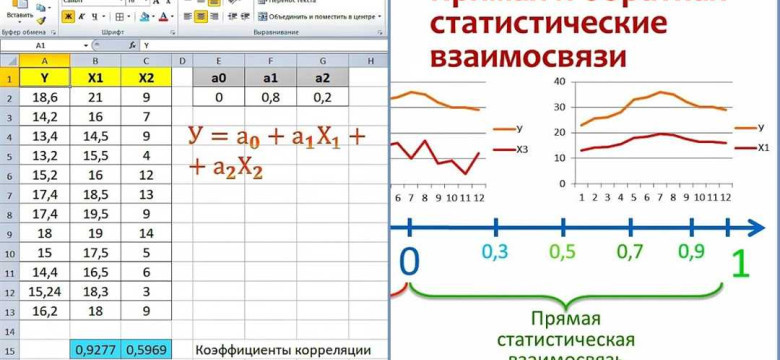
Используя программное обеспечение для статистического анализа, можно рассчитать коэффициент множественной корреляции, чтобы определить, насколько хорошо значения независимых переменных (X1 и X2) объясняют значения зависимой переменной (Y) в данном примере.
Коэффициент множественной детерминации: основные аспекты и интерпретация
Множественная детерминация является расширением и развитием понятия множественной корреляции, которая измеряет силу и направление связи между независимыми и зависимой переменными. Коэффициент множественной детерминации позволяет определить, какой процент изменчивости зависимой переменной может быть объяснен совокупностью независимых переменных, участвующих в модели.
Значение коэффициента множественной детерминации может варьироваться от 0 до 1. Значение 0 означает, что независимые переменные не объясняют изменчивость зависимой переменной, а значение 1 означает, что все изменчивость объясняется независимыми переменными. Чем ближе значение R^2 к 1, тем сильнее связь между независимыми и зависимой переменными, и тем лучше модель объясняет изменения зависимой переменной.
Интерпретация коэффициента множественной детерминации зависит от конкретного контекста и предметной области исследования. Высокое значение R^2 может указывать на сильную связь между переменными и возможность использования модели в прогнозных целях. Однако не следует забывать о возможности наличия других факторов, которые также могут влиять на зависимую переменную, но не участвовали в модели.
Важно учитывать, что множественная детерминация не является показателем причинно-следственной связи между переменными, а лишь позволяет измерить объяснительную способность модели. Интерпретацию коэффициента множественной детерминации нужно проводить с осторожностью, учитывая контекст и возможные ограничения исследования.
Множественный коэффициент корреляции: как он отличается от других видов корреляции?
В отличие от парной корреляции, где изучается связь между двумя переменными, множественный коэффициент корреляции позволяет изучать связь между зависимой переменной и множеством независимых переменных одновременно. Он позволяет определить взаимосвязь между переменными, при условии, что все независимые переменные учтены.
Основное отличие множественной корреляции от других видов корреляции заключается в том, что множественный коэффициент корреляции позволяет учитывать весь комплекс факторов, которые могут влиять на зависимую переменную. Таким образом, он предоставляет более полное представление о взаимосвязи между переменными, чем парная корреляция.
Одним из важных понятий, связанных с множественной корреляцией, является коэффициент множественной детерминации. Этот коэффициент представляет собой долю дисперсии зависимой переменной, объясненную независимыми переменными. Он позволяет оценить, насколько хорошо независимые переменные объясняют изменчивость зависимой переменной.
Таким образом, множественный коэффициент корреляции является мощным инструментом для изучения взаимосвязи между множеством независимых переменных и зависимой переменной. Он позволяет учесть все факторы, которые могут влиять на зависимую переменную, и предоставляет более полное представление о связи между переменными, чем парная корреляция.
Программы для расчета множественной корреляции: основные возможности и применение
Для расчета и анализа множественной корреляции существует несколько программных инструментов, которые предлагают различные функциональные возможности.
1. SPSS (Statistical Package for the Social Sciences)
SPSS является одной из самых популярных программ для статистического анализа данных. Она предоставляет множество функций для расчета множественной корреляции, включая расчет коэффициента детерминации, проверку статистической значимости и визуализацию результатов.
2. R
R - это свободно распространяемая среда программирования и язык для статистического анализа данных. Он также обладает широким набором инструментов для расчета множественной корреляции, включая различные пакеты, такие как "psych" и "corrplot". R также предоставляет возможность создания графиков и визуализации результатов.
Кроме SPSS и R, существуют и другие программы для расчета множественной корреляции, такие как SAS, MATLAB и Excel с использованием аналитического инструмента "Data Analysis". Каждая из этих программ имеет свои особенности и преимущества, поэтому выбор определенного инструмента зависит от потребностей и предпочтений исследователя.
Применение множественной корреляции в исследованиях может быть разнообразным. Она часто используется в психологии, социологии, экономике и других областях для исследования взаимосвязи между различными переменными, позволяя получить более глубокое понимание их взаимодействия. Например, множественная корреляция может быть использована для определения факторов, влияющих на успех студентов в учебе, с учетом таких переменных, как их уровень интеллекта и уровень образования родителей.
Таким образом, программы для расчета множественной корреляции представляют собой ценный инструмент для анализа данных и получения качественного и объективного вывода о взаимосвязях между переменными. Выбор конкретного программного средства зависит от потребностей исследователя, доступности и знакомства с определенным инструментом.
Способы расчета коэффициента множественной корреляции в программе [Название программы]
Существует несколько способов расчета коэффициента множественной корреляции в программе [Название программы]. Вот некоторые из них:
1. Методнаименование_1:
Описание расчета с использованием метода наименование_1 в программе [Название программы].
2. Методнаименование_2:
Описание расчета с использованием метода наименование_2 в программе [Название программы].
3. Методнаименование_3:
Описание расчета с использованием метода наименование_3 в программе [Название программы].
Каждый из этих способов имеет свои особенности и может быть предпочтительным в зависимости от конкретной задачи или предпочтений исследователя. В программе [Название программы] можно выбрать наиболее удобный и соответствующий целям анализа способ расчета коэффициента множественной корреляции.
Расчет коэффициента множественной корреляции в программе [Название программы] позволяет получить точную и надежную оценку связи между зависимой и независимыми переменными. Это позволяет более глубоко понять влияние независимых переменных на зависимую переменную и сделать выводы о важности каждой из них в объяснении вариации зависимой переменной.
Особенности интерпретации коэффициента множественной корреляции в [Название программы]
Коэффициент множественной корреляции часто обозначается как R или R-квадрат и представляет собой значения от 0 до 1. Значение ближе к 1 указывает на сильную положительную корреляцию между независимыми и зависимой переменными, в то время как значение ближе к 0 указывает на слабую или отсутствующую корреляцию. При интерпретации значений коэффициента множественной корреляции в [Название программы] следует учесть несколько особенностей:
- Коэффициент множественной корреляции может быть интерпретирован как доля детерминации, то есть процент вариации зависимой переменной, который объясняется независимыми переменными, участвующими в модели. Например, если коэффициент множественной корреляции равен 0,8, то 80% вариации зависимой переменной объясняется независимыми переменными.
- Знак коэффициента множественной корреляции указывает на направление связи между независимыми и зависимой переменными. Положительный знак означает прямую пропорциональность, тогда как отрицательный знак указывает на обратную пропорциональность.
- Коэффициент множественной корреляции не всегда указывает на причинно-следственные связи между переменными. Он лишь показывает, насколько хорошо независимые переменные предсказывают зависимую переменную.
При выполнении анализа с использованием [Название программы] и интерпретации коэффициента множественной корреляции следует учитывать эти особенности. Это позволит более точно оценить взаимосвязь между переменными и сделать выводы о влиянии независимых переменных на зависимую переменную.
Как использовать коэффициент множественной корреляции в практической работе?
1. Анализ данных

Коэффициент множественной корреляции позволяет исследовать степень зависимости между несколькими переменными. Путем анализа этого коэффициента можно выявить тесные связи и взаимодействия между переменными. Например, при изучении влияния различных факторов на продажи товаров, коэффициент множественной корреляции поможет определить, какие факторы оказывают самое сильное влияние.
2. Прогнозирование
Коэффициент множественной корреляции может быть использован для прогнозирования значений зависимой переменной на основе значений независимых переменных. Это позволяет установить математическую модель, которая может быть использована для предсказания будущих результатов или трендов. Например, зная значения объёма продаж, цены и расходов на рекламу, можно внедрить модель, которая позволит предсказывать продажи товара в будущем.
Коэффициент множественной корреляции является мощным инструментом в анализе данных и позволяет получать глубокие и полезные результаты. Однако, при его использовании необходимо учитывать, что корреляция не всегда означает причинно-следственную связь между переменными, а только указывает на наличие статистически значимой зависимости. Поэтому, при интерпретации результатов необходимо быть осторожным и проводить дополнительные исследования для подтверждения полученных выводов.
Рекомендации по расчету и использованию коэффициента множественной корреляции в научных исследованиях
Для расчета коэффициента множественной корреляции необходимо иметь данные по зависимой переменной и двум или более независимым переменным. Формула для расчета коэффициента множественной корреляции включает в себя вычисление корреляций между каждой парой переменных и корреляций между каждой из независимых переменных и зависимой переменной.
Получив значение коэффициента множественной корреляции, можно проанализировать его интерпретацию. Коэффициент может принимать значения от -1 до 1. Значение 0 означает отсутствие связи между переменными, а значения -1 или 1 указывают на наличие сильной отрицательной или положительной связи между ними.
Использование коэффициента множественной корреляции имеет свои преимущества и ограничения. Он позволяет определить, насколько хорошо независимые переменные объясняют вариацию зависимой переменной в модели множественной регрессии. Коэффициент множественной корреляции также может быть использован для прогнозирования значений зависимой переменной на основе значений независимых переменных.
Однако, при интерпретации коэффициента множественной корреляции важно учитывать, что он не обязательно указывает на причинно-следственную связь между переменными. Также следует учитывать возможность наличия факторов, которые не были включены в модель и могут влиять на исследуемые переменные.
Краткие рекомендации по использованию коэффициента множественной корреляции:
- Проверьте предварительные условия для использования коэффициента множественной корреляции, такие как нормальность распределения переменных и линейность связи.
- Оцените коэффициенты корреляции между каждой парой переменных и между каждой из независимых переменных и зависимой переменной.
- Рассчитайте коэффициент множественной корреляции, используя формулу и полученные значения корреляций.
- Интерпретируйте полученное значение коэффициента множественной корреляции в контексте исследования.
- Учитывайте ограничения и предположения, связанные с использованием коэффициента множественной корреляции.
Таким образом, коэффициент множественной корреляции является полезным инструментом для изучения взаимосвязи между переменными в научных исследованиях. Его использование требует тщательного расчета и интерпретации, а также учета предположений и ограничений модели.
Видео:
Как вычислить линейный коэффициент корреляции по таблице? Корреляционное поле и прямая регрессии
Как вычислить линейный коэффициент корреляции по таблице? Корреляционное поле и прямая регрессии by Mathprofi ru com 2,635 views 1 year ago 11 minutes, 51 seconds
Преобразование выражений, содержащих кв.корни. Внесение и вынесения из, под знак кв. корня. 8 класс.
Преобразование выражений, содержащих кв.корни. Внесение и вынесения из, под знак кв. корня. 8 класс. by MEKTEП OnLine MATEMATИKA 93,988 views 3 years ago 11 minutes, 13 seconds
Вопрос-ответ:
Что такое коэффициент множественной корреляции?
Коэффициент множественной корреляции представляет собой меру силы и направления связи между зависимой переменной и набором независимых переменных.
Как рассчитать коэффициент множественной корреляции?
Для расчета коэффициента множественной корреляции необходимо использовать метод множественной регрессии. Данный метод позволяет определить взаимозависимость между зависимой переменной и независимыми переменными путем построения уравнения регрессии и вычисления коэффициентов при независимых переменных.