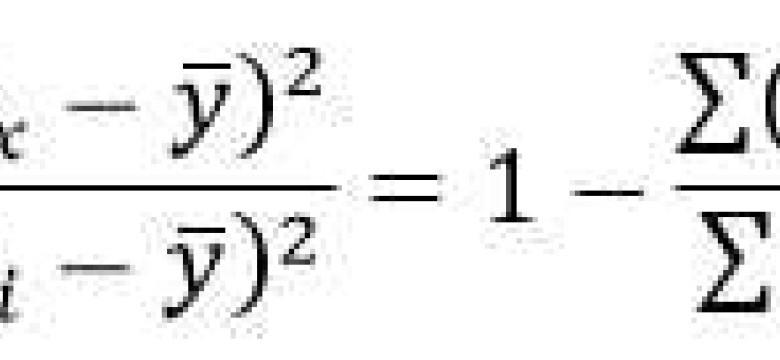
Коэффициент детерминации является одним из главных показателей в статистике, который используется для измерения степени связи между двумя переменными. Он позволяет определить, насколько хорошо некая зависимая переменная Y (например, выходной коэффициент в экономической модели) может быть предсказана с помощью независимой переменной X (например, уровень инвестиций).
Для вычисления коэффициента детерминации используется формула, которая основана на коэффициенте корреляции Пирсона, который показывает меру линейной зависимости между двумя переменными. Коэффициент корреляции Пирсона может принимать значения от -1 до 1, где значение 1 означает идеальную прямую линейную зависимость, значение -1 - идеальную обратную линейную зависимость, а значение 0 - отсутствие линейной зависимости.
Расчет коэффициента детерминации основан на предсказываемых значениях зависимой переменной, полученных с помощью модели линейной регрессии. Путем сравнения этих предсказанных значений с средним значением зависимой переменной можно определить, какая часть ее изменчивости объяснена моделью.
Формула расчета коэффициента детерминации в случае множественной линейной регрессии выглядит следующим образом:
Что такое коэффициент детерминации и его значение в анализе данных
В случае множественной регрессии, коэффициент детерминации показывает, насколько успешно независимые переменные объясняют вариацию зависимой переменной. Значение коэффициента детерминации может находиться в диапазоне от 0 до 1, и чем ближе значение к 1, тем лучше модель объясняет вариацию данных.
Формула для расчета коэффициента детерминации основана на коэффициенте корреляции Пирсона. Для расчета коэффициента детерминации используется следующая формула:
Формула коэффициента детерминации:

R2 = r2
где R - коэффициент детерминации, r - коэффициент корреляции Пирсона.
Значение коэффициента детерминации можно интерпретировать следующим образом:
- R2 < 0.3: модель не очень хорошо объясняет вариацию данных;
- 0.3 < R2 < 0.7: модель достаточно хорошо объясняет вариацию данных;
- R2 > 0.7: модель очень хорошо объясняет вариацию данных.
Таким образом, коэффициент детерминации является важным инструментом в анализе данных, позволяющим оценивать качество модели и ее способность объяснить наблюдаемую вариацию.
Формула расчета коэффициента детерминации в программе

Формула расчета коэффициента детерминации основана на коэффициенте корреляции Пирсона. Для его вычисления необходимо знать значения независимых переменных (x) и соответствующие значения зависимой переменной (y).
Формула выглядит следующим образом:
R2 = (cov(x,y) / (σx * σy))2
Где:
- R2 – коэффициент детерминации.
- cov(x,y) – ковариация между x и y.
- σx и σy – стандартные отклонения x и y, соответственно.
Для расчета коэффициента детерминации в программе необходимо подставить значения в формулу и выполнить необходимые математические операции. Результат будет указывать на то, насколько модель линейной регрессии хорошо описывает зависимость между переменными.
Коэффициент корреляции
В случае множественной регрессии, коэффициент корреляции множественной корреляции (R) является расширением понятия коэффициента корреляции Пирсона для более чем двух переменных. Он измеряет силу и направление связи между зависимой переменной и набором независимых переменных.
Формула для расчета коэффициента множественной корреляции состоит из двух частей. Сначала необходимо рассчитать коэффициент Пирсона между каждой парой переменных. Затем полученные значения корреляций нужно умножить на коэффициенты регрессии между зависимой переменной и каждой независимой переменной. После этого полученные произведения нужно сложить и получить окончательное значение коэффициента множественной корреляции.
Пример:
Рассмотрим следующий пример расчета коэффициента множественной корреляции:
| Зависимая переменная | Независимая переменная 1 | Независимая переменная 2 |
|---|---|---|
| X | Y | Z |
| 1 | 2 | 3 |
| 2 | 4 | 6 |
| 3 | 6 | 9 |
| 4 | 8 | 12 |
Для начала рассчитаем коэффициенты корреляции Пирсона между каждой переменной:
| X | Y | Z | |
|---|---|---|---|
| X | 1 | 0.993 | 0.997 |
| Y | 0.993 | 1 | 0.999 |
| Z | 0.997 | 0.999 | 1 |
Затем рассчитаем коэффициенты регрессии для каждой переменной:
| Зависимая переменная | Коэффициент регрессии |
|---|---|
| X | 0.25 |
| Y | 0.5 |
| Z | 0.75 |
Наконец, умножим каждый коэффициент корреляции на соответствующий коэффициент регрессии и сложим полученные произведения:
R = (0.993 * 0.25) + (0.999 * 0.5) + (0.997 * 0.75) = 0.99325
Таким образом, коэффициент множественной корреляции для этого примера равен 0.99325.
Как определить степень взаимосвязи между двумя переменными
Коэффициент детерминации используется для оценки степени взаимосвязи между двумя переменными. Если мы имеем дело с зависимостью между одной зависимой переменной и несколькими независимыми переменными, то используется множественная коэффициент детерминации.
Множественная коэффициент детерминации показывает, насколько хорошо линейная модель, использующая несколько независимых переменных, объясняет вариацию зависимой переменной. Он также может быть интерпретирован как доля объясненной дисперсии зависимой переменной.
Формула множественной коэффициента детерминации
Множественный коэффициент детерминации обозначается как R2 и может быть рассчитан по следующей формуле:
R2 = 1 - (SSR / SST)
где SSR - сумма квадратов остатков, SST - общая сумма квадратов.
Интерпретация множественного коэффициента детерминации
Значение множественного коэффициента детерминации лежит в диапазоне от 0 до 1. Ближе к 1 оно указывает на более сильную взаимосвязь между независимыми и зависимой переменными. Значение множественного коэффициента детерминации равное 0 говорит о том, что модель не объясняет вариацию зависимой переменной никакими факторами.
Несмотря на то, что множественный коэффициент детерминации позволяет определить взаимосвязь между переменными, он не даёт информации о причинно-следственной связи. Для этого нужно обратиться к другим методам оценки зависимостей, таким как коэффициент корреляции Пирсона.
Коэффициент множественной корреляции
Коэффициент множественной корреляции, также известный как коэффициент Пирсона, представляет собой статистическую метрику, которая позволяет оценить степень взаимосвязи между несколькими переменными. Он используется для измерения силы и направления линейной зависимости между этими переменными.
Формула для расчета коэффициента множественной корреляции основана на формуле коэффициента Пирсона (также называемого коэффициентом корреляции). Однако, в случае множественной корреляции, мы имеем несколько предикторов (или независимых переменных), поэтому нужно учитывать их влияние на зависимую переменную.
Формула для расчета коэффициента множественной корреляции выглядит следующим образом:
Коэффициент множественной корреляции (R) = sqrt(кв. корень (R^2))
где:
- R - коэффициент множественной корреляции
- R^2 - коэффициент детерминации
Коэффициент множественной корреляции находится в диапазоне от -1 до 1. Значение ближе к -1 указывает на обратную корреляцию между переменными, значение ближе к 1 указывает на прямую корреляцию, а значение близкое к 0 указывает на отсутствие линейной зависимости.
Таким образом, коэффициент множественной корреляции позволяет оценить силу и направление связи между несколькими переменными и помогает в исследованиях, где требуется учитывать влияние нескольких факторов на исследуемый процесс или явление.
В чем отличие от коэффициента корреляции и как вычислить
Отличие коэффициента детерминации от коэффициента корреляции состоит в их предназначении и расчете. Коэффициент корреляции, такой как коэффициент Пирсона, измеряет степень линейной связи между двумя переменными. Он может быть вычислен для одной или нескольких пар переменных.
Коэффициент детерминации, с другой стороны, применяется в случае множественной регрессии, когда имеется несколько независимых переменных, которые объясняют вариацию зависимой переменной. Он показывает, какую долю общей вариации объясняют все независимые переменные вместе.
Формула для расчета коэффициента детерминации основана на разделении суммы квадратов изменения зависимой переменной на две части: объясненную и необъясненную. Объясненная часть связана с воздействием независимых переменных, а необъясненная со случайными факторами.
| Обозначение | Описание |
|---|---|
| SST | Общая сумма квадратов |
| SSR | Объясненная сумма квадратов (сумма квадратов регрессии) |
| SSE | Необъясненная сумма квадратов (остаточная сумма квадратов) |
Формула для коэффициента детерминации:
R-квадрат = SSR / SST = 1 - SSE / SST
Вычисленная величина коэффициента детерминации находится в диапазоне от 0 до 1. Значение 0 указывает на то, что модель не объясняет вариацию зависимой переменной, а значение 1 означает ее полное объяснение.
Коэффициент Пирсона
Формула расчета коэффициента Пирсона выглядит следующим образом:
| rxy = | Σ((xi - x̄)(yi - ȳ)) / √((Σ(xi - x̄)2) * (Σ(yi - ȳ)2)) |
Здесь:
- rxy - коэффициент Пирсона;
- xi и yi - значения переменных x и y соответственно;
- x̄ и ȳ - средние значения переменных x и y соответственно.
Коэффициент Пирсона может принимать значения от -1 до 1. Значение -1 указывает на полную отрицательную линейную связь, 0 - на отсутствие линейной связи, а 1 - на положительную линейную связь.
Как применяется в статистическом анализе данных
Для применения коэффициента детерминации в статистическом анализе данных необходимо иметь пары переменных, которые предполагается исследовать на корреляцию и взаимосвязь. Обычно, эти данные представлены в виде таблицы, где каждая строка содержит значения двух переменных.
Коэффициент детерминации рассчитывается как квадрат множественного коэффициента корреляции, также известного как коэффициент Пирсона. Для его расчета используется специальная формула, которая учитывает соотношение суммы квадратов отклонений зависимой переменной от ее среднего значения к сумме квадратов отклонений зависимой переменной от значений, предсказанных моделью.
Видео:
Коэффициент корреляции Пирсона, 2 способа вычисления
Коэффициент корреляции Пирсона, 2 способа вычисления by Аграрёк 15,997 views 3 years ago 5 minutes, 18 seconds
Вопрос-ответ:
Что такое коэффициент детерминации и для чего он используется?
Коэффициент детерминации - это статистическая мера, которая показывает, насколько хорошо прогнозируемая переменная (зависимая переменная) может быть объяснена или предсказана с помощью независимых переменных. Он указывает на долю вариации зависимой переменной, которая может быть объяснена или предсказана с помощью независимых переменных. Коэффициент детерминации обычно выражается в процентах и принимает значения от 0 до 100%. Чем ближе значение коэффициента детерминации к 100%, тем лучше модель объясняет зависимую переменную.
Как вычислить коэффициент детерминации?
Для вычисления коэффициента детерминации необходимо использовать формулу: R^2 = (SSR / SST), где SSR - сумма квадратов отклонений (regression sum of squares), которая представляет собой сумму квадратов разницы между прогнозируемыми значениями и средним значением зависимой переменной, SST - полная сумма квадратов (total sum of squares), которая представляет собой сумму квадратов разницы между наблюдаемыми значениями и средним значением зависимой переменной. Значение коэффициента детерминации будет находиться в диапазоне от 0 до 1. Для получения значения в процентах нужно умножить на 100.
Что такое коэффициент множественной корреляции?
Коэффициент множественной корреляции является мерой силы и направления линейной связи между зависимой переменной и набором независимых переменных. Он указывает, насколько хорошо независимые переменные объясняют вариацию зависимой переменной. Значение коэффициента множественной корреляции может варьироваться от -1 до 1, где -1 указывает на полную отрицательную корреляцию, 1 указывает на положительную корреляцию, а 0 указывает на отсутствие корреляции.
Можно ли с помощью коэффициента детерминации определить, насколько точно математическая модель описывает данные?
Да, коэффициент детерминации позволяет определить долю вариации зависимой переменной, которую можно объяснить с помощью независимых переменных. Если коэффициент детерминации равен 1, это значит, что модель полностью описывает данные и доля объясненной вариации равна 100%. Если коэффициент детерминации близок к нулю, это говорит о том, что модель плохо описывает данные и доля объясненной вариации очень низкая.
Как вычислить коэффициент корреляции Пирсона?
Для вычисления коэффициента корреляции Пирсона необходимо использовать следующую формулу: r = (Σ(xi - x̄)(yi - ȳ)) / √((Σ(xi - x̄)^2) * (Σ(yi - ȳ)^2)), где xi и yi - значения переменных x и y соответственно, x̄ и ȳ - средние значения переменных x и y.