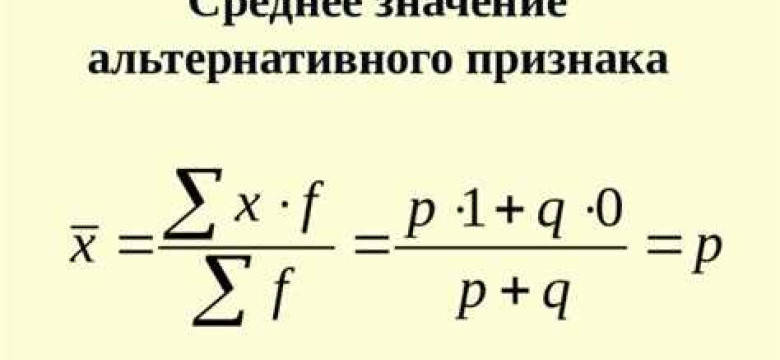
Среднее значение, также известное как арифметическое среднее или математическое ожидание, является одной из наиболее распространенных и важных функций в математике и статистике. Эта функция позволяет нам вычислить среднее значение набора чисел, определяя их сумму и количество.
Для вычисления среднего значения мы суммируем все числа в наборе и делим результат на количество чисел. Это позволяет нам определить среднее значение и понять, каково среднее значение данного набора данных. Например, если у нас есть набор чисел {2, 4, 6, 8, 10}, мы можем вычислить среднее значение, сложив все числа и разделив результат на 5, потому что в наборе 5 чисел.
Формула для вычисления среднего значения:
Среднее значение = сумма всех чисел / количество чисел
Понимание среднего значения имеет большое значение для различных областей, включая науку, экономику, программирование и многое другое. Эта функция используется для анализа данных, сравнения результатов и принятия решений на основе средних значений. Например, в финансовой сфере оно может помочь определить средний доход или потери, а в медицине - среднюю долю успеха лечения определенного заболевания.
Среднее значение формула: как вычислить и использовать
Для вычисления среднего значения используется следующая формула:
Среднее значение = сумма значений / количество значений
Для примера, рассмотрим набор чисел: 5, 8, 12, 4, 10.
Сначала нужно найти сумму всех значений:
5 + 8 + 12 + 4 + 10 = 39
Затем нужно поделить полученную сумму на количество значений, в данном случае 5:
39 / 5 = 7.8
Таким образом, среднее значение для данного набора чисел равно 7.8.
Среднее значение имеет множество применений в различных областях. Например, оно может использоваться для нахождения среднего возраста людей в определенной группе, средней оценки по предмету или среднего времени выполнения задачи.
Примеры использования среднего значения:
1. В медицине: среднее значение может помочь определить среднюю длительность болезни у пациентов и выбрать наиболее эффективное лечение.
2. В экономике: среднее значение может быть использовано для расчета средней зарплаты в определенном регионе или для оценки средней стоимости товара.
3. В статистике: среднее значение является одной из основных характеристик распределения данных и может использоваться для анализа и сравнения разных выборок.
Использование среднего значения позволяет получить общую картину или оценку исследуемой величины, усредненную по всем ее значениям.
Таблица с примером вычисления среднего значения:
| Значения | Сумма значений | Количество значений | Среднее значение |
|---|---|---|---|
| 5, 8, 12, 4, 10 | 39 | 5 | 7.8 |
Программы для вычисления среднего значения
Для вычисления среднего значения существует несколько программных реализаций, которые предлагают различные методы и формулы для расчета.
1. Математическое ожидание
Математическое ожидание - это среднее арифметическое значений случайной величины, умноженных на их вероятности. Для вычисления математического ожидания можно использовать специализированные программные пакеты, такие как Matlab, R или Python с библиотекой numpy.
2. Арифметическое среднее значение
Арифметическое среднее значение - это простейший способ определения среднего значения, когда все значения складываются и делятся на их количество. Для вычисления арифметического среднего значения можно использовать различные программы, такие как Microsoft Excel, Google Sheets или программы для статистического анализа данных, например, SPSS или SAS.
Роль среднего значения в статистике
Математическое ожидание - это функция, которая вычисляет среднее арифметическое значение случайной величины. Формула для вычисления математического ожидания зависит от типа распределения случайной величины. Например, для дискретной случайной величины формула имеет вид:
| Распределение | Формула для математического ожидания |
|---|---|
| Равномерное | Математическое ожидание = (a + b) / 2 |
| Биномиальное | Математическое ожидание = n * p |
| Нормальное | Математическое ожидание = μ |
Среднее значение имеет важное значение в статистике: оно позволяет оценить центральную тенденцию данных. Если значения случайной величины близки к ее среднему значению, то можно сделать вывод, что данные в целом сосредоточены вокруг этого значения. Однако, среднее значение может быть подвержено влиянию выбросов или экстремальных значений, поэтому при его интерпретации следует учитывать и другие характеристики распределения данных.
Таким образом, среднее значение является важной характеристикой случайной величины и используется для анализа и описания данных в статистике.
Математическое ожидание
Арифметическое ожидание функции f(X) определяется с использованием формулы:
E[f(X)] = ∑ f(x) * P(X=x)
где E[f(X)] - математическое ожидание функции, f(X) - функция, определенная на множестве возможных значений X, x - значения X, P(X=x) - вероятность получения значения x.
Математическое ожидание может использоваться в различных областях, таких как физика, экономика, социология и др. Оно позволяет предсказать среднее значение некоторого свойства или явления на основе имеющихся данных. Например, в экономике, математическое ожидание может использоваться для прогнозирования дохода или потерь компании, исходя из исторических данных.
Пример
Рассмотрим следующий пример: у нас есть набор данных о доходах 10 человек. Допустим, что эти доходы равновероятно распределены от 10 000 до 50 000 рублей. Мы можем использовать математическое ожидание для определения среднего дохода в этой выборке.
| Доход | Вероятность | f(Доход) | f(Доход) * Вероятность |
|---|---|---|---|
| 10 000 | 1/10 | 10 000 | 10 000 * 1/10 = 1 000 |
| 20 000 | 1/10 | 20 000 | 20 000 * 1/10 = 2 000 |
| 30 000 | 1/10 | 30 000 | 30 000 * 1/10 = 3 000 |
| 40 000 | 1/10 | 40 000 | 40 000 * 1/10 = 4 000 |
| 50 000 | 1/10 | 50 000 | 50 000 * 1/10 = 5 000 |
| Сумма: | 15 000 | ||
Таким образом, средний доход в этой выборке составляет 15 000 рублей.
Определение и основные свойства
Математическое ожидание имеет несколько свойств, которые делают его полезным в различных областях. Во-первых, оно является линейной функцией, то есть среднее значение суммы двух функций равно сумме их средних значений. Во-вторых, при умножении функции на константу, среднее значение этой функции также умножается на эту константу. Наконец, среднее значение функции может быть использовано для вычисления вероятности или среднего значения случайной величины.
| Свойство | Описание |
| Линейность | Среднее значение суммы двух функций равно сумме их средних значений |
| Умножение на константу | При умножении функции на константу, среднее значение этой функции также умножается на эту константу |
Применение математического ожидания в теории вероятностей
Математическое ожидание вычисляется с помощью арифметической формулы, которая основывается на усреднении всех возможных значений случайной величины. Для дискретной случайной величины формула выглядит следующим образом:
Математическое ожидание (среднее значение) = Σ(значение * вероятность)
Здесь Σ обозначает сумму, значение - возможное значение случайной величины, а вероятность - вероятность появления данного значения.
Применение математического ожидания в теории вероятностей позволяет решать различные задачи. Например, посчитав математическое ожидание можно определить среднюю оценку студента за экзамен, среднюю прибыль предприятия или среднюю продолжительность жизни людей в определенной стране.
Кроме того, математическое ожидание используется для вычисления других статистических параметров, таких как дисперсия (мера разброса значений вокруг математического ожидания) и стандартное отклонение (квадратный корень из дисперсии).
Таким образом, математическое ожидание является одним из основных инструментов в теории вероятностей и статистике, позволяющим определить среднее значение и предсказать ожидаемый результат на основе вероятностных данных.
Среднее арифметическое
Среднее арифметическое = (Сумма всех чисел) / (Количество чисел)
Например, для набора чисел 2, 4, 6, 8, 10, сумма этих чисел равна 30, а количество чисел равно 5. Подставляя эти значения в формулу, получаем:
Среднее арифметическое = 30 / 5 = 6
Таким образом, среднее арифметическое для данного набора чисел равно 6. Среднее арифметическое может быть использовано для определения типичного значения в наборе данных и помогает в анализе и интерпретации результатов.
Как вычислить среднее арифметическое
Среднее арифметическое, также известное как среднее значение, вычисляется путем суммирования всех чисел и деления полученной суммы на их количество. Формула для вычисления среднего арифметического выглядит следующим образом:
Среднее арифметическое = сумма всех чисел / количество чисел
Например, если у нас есть последовательность чисел 3, 5, 8, 12, то сначала мы их суммируем:
3 + 5 + 8 + 12 = 28
Затем делим полученную сумму на количество чисел в последовательности, в данном случае 4:
28 / 4 = 7
Таким образом, среднее арифметическое для данной последовательности чисел равно 7.
Примеры использования среднего арифметического
Среднее арифметическое, также известное как среднее значение или арифметическое ожидание, играет важную роль в математике и статистике. Это значение вычисляется по формуле, которая представляет собой сумму всех значений, разделенную на их количество.
Среднее арифметическое может быть использовано для различных целей, включая:
1. Анализ данных
Среднее арифметическое может быть использовано для анализа данных, исследования распределения значений и определения общей тенденции. Например, если имеется набор данных, обозначающих доходы работников компании, можно вычислить среднее арифметическое, чтобы определить средний доход сотрудников.
2. Прогнозирование будущих значений
Среднее арифметическое может быть использовано для прогнозирования будущих значений, основываясь на прошлых данных. Например, если имеется набор данных, отображающих продажи товаров по месяцам, можно вычислить среднее арифметическое, чтобы предсказать средние продажи в будущем.
3. Сравнение значений
Среднее арифметическое может быть использовано для сравнения значений. Например, если имеется набор данных, представляющих оценки студентов по различным предметам, можно вычислить среднее арифметическое каждой группы и сравнить их между собой, чтобы определить, в какой группе оценки выше.
Все эти примеры демонстрируют полезность и важность среднего арифметического в различных областях. Оно помогает обрабатывать данные, делать прогнозы и сравнивать значения для принятия решений на основе математического ожидания.
Среднее значение функции
Формула для вычисления среднего значения функции на заданном промежутке выглядит следующим образом:
| Среднее значение функции | = | 1/(b-a) * ∫ab f(x) dx |
Где:
- a, b – границы заданного промежутка;
- f(x) – математическое значение функции на промежутке [a, b];
- ∫ab f(x) dx – интеграл функции f(x) на промежутке [a, b].
Вычисление среднего значения функции позволяет найти среднее арифметическое значение функции на заданном промежутке. Это может быть полезно, например, при анализе экономических показателей, прогнозировании результатов и других задачах.
Видео:
Среднее арифметическое и средневзвешенное значение. Mатематика 6 класс. Урок 6
Среднее арифметическое и средневзвешенное значение. Mатематика 6 класс. Урок 6 by Matematik Repetitor 2,909 views 1 year ago 4 minutes, 4 seconds
СРЗНАЧ, СТАНДОТКЛОН: Excel с нуля
СРЗНАЧ, СТАНДОТКЛОН: Excel с нуля by Excel с нуля 4,444 views 2 years ago 2 minutes, 30 seconds
Вопрос-ответ:
Как вычислить среднее значение?
Среднее значение можно вычислить, сложив все числа и разделив полученную сумму на их количество. Например, если у нас есть числа 1, 3, 5, для вычисления среднего значения нужно сложить эти числа (1+3+5=9) и разделить полученную сумму на их количество (9/3=3). Таким образом, среднее значение этой последовательности чисел равно 3.
Что такое среднее арифметическое?
Среднее арифметическое - это сумма всех чисел, деленная на их количество. Это часто используемая статистическая мера центральной тенденции. Например, если у нас есть числа 1, 2, 3, 4, среднее арифметическое будет равно (1+2+3+4)/4=2.5.
Как использовать среднее значение функции?
Среднее значение функции может быть использовано для разных целей. Например, оно может быть использовано для определения среднего значения измерений или для нахождение точки, в которой функция принимает среднее значение. Это также может быть полезно в анализе данных и предсказании трендов.
Что такое математическое ожидание?
Математическое ожидание - это среднее значение случайной величины, которое можно рассчитать, умножив каждое возможное значение на его вероятность и сложив все результаты. В контексте вероятности и статистики, математическое ожидание может представлять собой предсказание наиболее вероятного значения или среднего значения случайного события.