Коэффициент детерминации (R-квадрат) является мерой зависимости переменной от другой переменной. Однако обычный R-квадрат может быть искажен из-за наличия лишних факторов, что вносит неточности в результаты исследования. Решением этой проблемы является использование скорректированного коэффициента детерминации (R-квадрат с поправкой), который учитывает количество предикторов в модели.
Скорректированный R-квадрат позволяет оценить, насколько хорошо модель описывает данные, учитывая число независимых переменных. Он может принимать значения от 0 до 1, где 0 означает, что модель не объясняет колебания зависимой переменной, а 1 - полное объяснение. Чем ближе значение коэффициента к 1, тем лучше модель описывает данные.
Формула для расчета скорректированного R-квадрата: Корректированный R-квадрат = 1 - ((1 - R^2) * (n - 1) / (n - k - 1)), где R^2 - обычный коэффициент детерминации, n - количество наблюдений, k - количество независимых переменных.
Использование скорректированного R-квадрата позволяет более объективно оценить вклад независимых переменных в объяснение изменений зависимой переменной, что очень полезно при статистическом анализе данных и построении моделей. Этот показатель помогает учитывать сложности, связанные с увеличением числа предикторов и делает оценку регрессии более точной и надежной.
Скорректированный коэффициент детерминации: формула и применение
Формула скорректированного коэффициента детерминации
Исправленный (скорректированный) r-квадрат вычисляется по следующей формуле:
r-квадрат, с поправкой = 1 - [(1 - r-квадрат) * (n - 1) / (n - k - 1)]
где:
- r-квадрат - оригинальный коэффициент детерминации
- n - общее число наблюдений
- k - число факторов (предикторов) включенных в модель
Формула позволяет скорректировать коэффициент детерминации, учитывая число факторов в модели и число наблюдений. Скорректированный коэффициент детерминации находится в диапазоне от 0 до 1, и чем он ближе к 1, тем лучше модель объясняет вариацию зависимой переменной с учетом числа факторов.
Применение скорректированного коэффициента детерминации
Скорректированный коэффициент детерминации является более надежной мерой качества модели, так как учитывает число факторов и число наблюдений. Он позволяет сравнивать различные модели, учитывая их сложность и количество данных, используемых для оценки модели.
Высокое значение скорректированного r-квадрата может свидетельствовать о том, что модель хорошо соответствует данным и предсказывает вариацию зависимой переменной. Низкое значение может указывать на недостаточное количество факторов или на плохое соответствие модели данным.
Использование скорректированного коэффициента детерминации позволяет более точно оценить качество модели и принять решение о ее использовании или улучшении.
Исправленный коэффициент детерминации
Обычный коэффициент детерминации (R-квадрат) измеряет, насколько хорошо модель подходит для данных, но не учитывает количество предикторов в модели. Исправленный коэффициент детерминации с поправкой на количество предикторов позволяет сравнивать модели с разным числом переменных и учитывает степень свободы модели.
Формула для расчета исправленного коэффициента детерминации:
R-квадрат с поправкой = (1 - ((1 - R-квадрат) * ((n - 1) / (n - k - 1)))) * 100%
Где:
- R-квадрат - обычный коэффициент детерминации
- n - количество наблюдений
- k - количество независимых переменных в модели
Таким образом, исправленный коэффициент детерминации принимает значения от 0 до 100%, где более высокие значения указывают на более точную модель с меньшей ошибкой предсказания.
Исправленный коэффициент детерминации является полезным инструментом для оценки качества регрессионной модели и сравнения разных моделей с учетом количества независимых переменных. Он позволяет учесть сложность модели и определить, насколько хорошо она объясняет вариацию зависимой переменной.
Скорректированный R-квадрат
Коэффициент R-квадрат детерминации показывает, насколько вариации зависимой переменной может быть объяснена с помощью предикторов в модели. Он принимает значения от 0 до 1, где 0 означает, что модель не объясняет никакую вариацию, а 1 означает, что модель полностью объясняет всю вариацию. Однако коэффициент R-квадрат обычно склонен быть завышенным при добавлении новых предикторов, поэтому для корректной оценки модели используется скорректированный R-квадрат.
Формула для вычисления скорректированного R-квадрата:
скорректированный R-квадрат = 1 - [(1 - r-квадрат) * (n - 1) / (n - p - 1)],
где r-квадрат - это коэффициент детерминации, n - количество наблюдений и p - количество предикторов в модели.
Скорректированный R-квадрат позволяет сравнивать модели с разным количеством предикторов и учитывать их влияние на объясняемую переменную. Чем ближе значение скорректированного R-квадрата к 1, тем лучше модель объясняет зависимую переменную.
Коэффициент детерминации с поправкой
Обычный коэффициент детерминации (R-квадрат) измеряет долю вариации зависимой переменной, которая объясняется регрессионной моделью. Однако этот показатель имеет недостаток - он всегда увеличивается при добавлении новых независимых переменных в модель, даже если эти переменные не имеют статистически значимого влияния на зависимую переменную.
Для учета числа предикторов в модели используется исправленный коэффициент детерминации. Он корректируется с использованием числа предикторов и обычно имеет более низкое значение, чем обычный R-квадрат. Исправленный коэффициент детерминации позволяет оценить вклад каждого предиктора, учитывая число предикторов в модели и их статистическую значимость.
Формула для расчета исправленного коэффициента детерминации:
Скорректированный R-квадрат = 1 - (1 - R-квадрат) * ((n - 1) / (n - k - 1)),
где n - количество наблюдений, k - количество независимых переменных в модели.
Исправленный коэффициент детерминации позволяет более точно оценить предсказательные возможности модели и принимать решения на основе этой информации. Чем ближе значение исправленного R-квадрата к 1, тем лучше модель объясняет зависимую переменную. Однако следует помнить, что исправленный коэффициент детерминации не гарантирует прямого причинно-следственного отношения между предикторами и зависимой переменной.
| R-квадрат | Исправленный R-квадрат |
|---|---|
| 0.75 | 0.72 |
| 0.80 | 0.76 |
| 0.85 | 0.80 |
Программы для расчета коэффициента детерминации
С помощью этого программного обеспечения можно провести статистический анализ данных и получить численное значение коэффициента детерминации, который измеряет степень связи между зависимой и независимыми переменными. При этом, если использовать исправленный коэффициент детерминации с поправкой, он будет более точно отражать реальную силу связи между переменными.
Исправленный коэффициент детерминации (с поправкой на число использованных предикторов) называется скорректированным коэффициентом детерминации или коэффициентом r-квадрат. Он учитывает число независимых переменных в модели и дает оценку доли дисперсии зависимой переменной, объясняемой уравнением регрессии.
В общем случае, чем ближе значение скорректированного коэффициента детерминации к единице, тем лучше модель описывает данные. Однако стоит учитывать, что его значение может быть и отрицательным, что указывает на то, что модель не объясняет данные лучше, чем случайная величина. В таких случаях может потребоваться пересмотр модели и включение дополнительных предикторов.
Сравнение скорректированного и обычного коэффициентов детерминации
Для того чтобы учесть количество независимых переменных и получить более точную оценку объясняющей способности модели, используется скорректированный коэффициент детерминации с поправкой (исправленный r-квадрат). Этот показатель с учетом количества предикторов в модели оценивает, насколько хорошо модель подходит к данным.
Формула для вычисления скорректированного коэффициента детерминации:
Исправленный r-квадрат = 1 - ((1 - r-квадрат) * (n - 1) / (n - k - 1)),
где r-квадрат - обычный коэффициент детерминации, n - количество наблюдений, k - количество независимых переменных.
Сравнение обычного и скорректированного коэффициентов детерминации позволяет оценить влияние добавления новых предикторов на объясняющую способность модели. Если при добавлении новых переменных скорректированный коэффициент детерминации значительно выше обычного коэффициента, это говорит о том, что новые переменные улучшили предсказательную силу модели. Если же скорректированный коэффициент детерминации близок к обычному, то новые переменные практически не оказывают влияния на объяснение зависимой переменной.
Таким образом, использование скорректированного коэффициента детерминации с поправкой позволяет более точно оценить объясняющую способность модели, учитывая количество независимых переменных. Исправленный r-квадрат предоставляет информацию о том, насколько хорошо модель подходит к данным и влиянии добавления новых переменных на объяснение зависимой переменной.
Применение скорректированного коэффициента детерминации в научных исследованиях
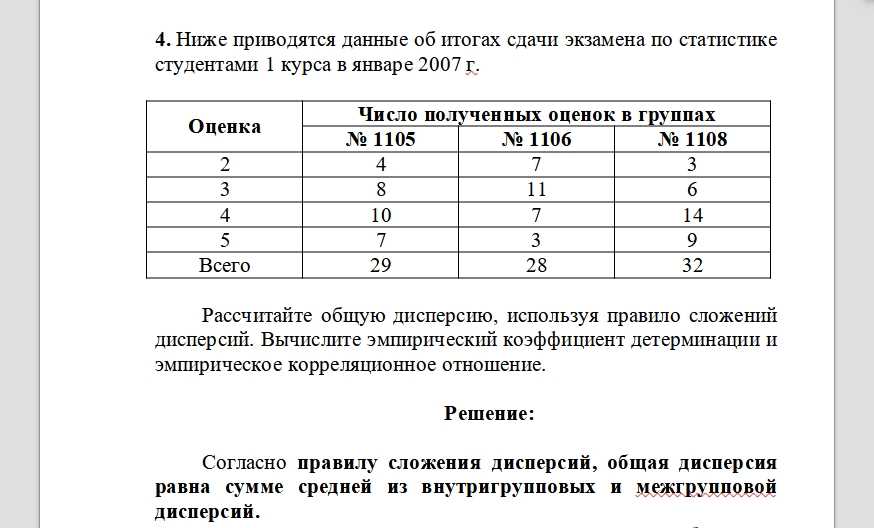
Скорректированный коэффициент детерминации (с) представляет собой исправленный вариант r-квадрат, который позволяет оценить прогностическую способность модели при наличии нескольких предикторов (регрессоров). Он вычисляется по формуле:
c = 1 - ((1 - r-квадрат) * (n - 1) / (n - k - 1))
где r-квадрат - обычный коэффициент детерминации, n - количество наблюдений, k - количество регрессоров (предикторов).
Применение скорректированного коэффициента детерминации в научных исследованиях заключается в его использовании для оценки качества моделей, предсказывающих зависимую переменную на основе набора предикторов. Он позволяет сравнить модели с разным количеством предикторов и выбрать наиболее подходящую модель с учетом количества наблюдений и степени свободы.
Коэффициент детерминации с поправкой является более консервативным и предпочтительным показателем качества модели, поскольку он контролирует вероятность переобучения и учитывает сложность модели. В научных исследованиях, где важна точность прогнозирования и обобщение результатов на другие выборки или ситуации, применение скорректированного коэффициента детерминации является важным элементом анализа данных.
Пример использования скорректированного коэффициента детерминации:

Рассмотрим исследование, где требуется предсказать уровень успеха студентов на основе различных факторов, таких как количество часов учебы, уровень знаний перед началом курса, возраст и пол. В данном случае мы имеем 100 наблюдений и 4 предиктора.
Мы построили несколько моделей, используя различные комбинации предикторов, и вычислили для каждой модели коэффициент детерминации. Однако, чтобы выбрать наилучшую модель с учетом количества предикторов и степени свободы, мы вычисляем скорректированный коэффициент детерминации используя формулу:
c = 1 - ((1 - r-квадрат) * (n - 1) / (n - k - 1))
После вычисления скорректированного коэффициента детерминации для всех моделей, мы можем сравнить их показатели и выбрать модель с наилучшей прогностической способностью, учитывая ограничения свободы и количество наблюдений.
Применение скорректированного коэффициента детерминации в исследованиях с большим количеством предикторов:
В некоторых научных исследованиях может потребоваться использование большого количества предикторов для предсказания зависимой переменной. В таких случаях, регулярный коэффициент детерминации может быть завышен, поскольку он учитывает все предикторы независимо от их влияния на зависимую переменную.
Поэтому, применение скорректированного коэффициента детерминации позволяет учесть сложность модели и количество предикторов, что делает его более интерпретируемым и надежным показателем в исследованиях с большим количеством предикторов.
| Модель | r-квадрат | Скорректированный коэффициент детерминации |
|---|---|---|
| Модель 1 | 0.75 | 0.71 |
| Модель 2 | 0.80 | 0.75 |
| Модель 3 | 0.85 | 0.80 |
В данном примере мы видим, что несмотря на то, что r-квадрат увеличивается с увеличением количества предикторов, скорректированный коэффициент детерминации также увеличивается, но в меньшей степени. Это указывает на то, что учет степени свободы и сложности модели дает более объективную оценку качества модели, а именно предсказательную способность.
Рекомендации по использованию скорректированного коэффициента детерминации
Однако, обычный R-квадрат имеет некоторые недостатки, особенно при наличии большого количества независимых переменных в модели. В таких случаях, скорректированный коэффициент детерминации с поправкой на число независимых переменных становится более применимым инструментом для оценки качества модели.
Применение скорректированного R-квадрата позволяет перейти от простого объяснения изменчивости зависимой переменной, к объяснению этой изменчивости, учитывая сложность модели и количество используемых независимых переменных. Скорректированный R-квадрат всегда будет меньше или равен обычному R-квадрату, поскольку он учитывает штраф за каждую добавленную независимую переменную.
Рекомендуется использовать скорректированный коэффициент детерминации вместо обычного R-квадрата, особенно при наличии большого количества независимых переменных, чтобы получить более точную оценку объясняющей способности модели. Однако следует учитывать, что скорректированный R-квадрат не является единственной мерой качества модели и должен использоваться в сочетании с другими статистическими показателями для полного анализа регрессии.
Видео:
Множественный и частные коэффициенты корреляции
Множественный и частные коэффициенты корреляции by Ольга Пашковская 553 views 1 year ago 31 minutes
Вопрос-ответ:
Зачем нужен скорректированный коэффициент детерминации?
Скорректированный коэффициент детерминации используется для оценки точности регрессионной модели при учете числа независимых переменных. Он позволяет сравнивать модели с разным количеством предикторов и выбирать наиболее подходящую модель.
Как вычисляется скорректированный коэффициент детерминации?
Формула для расчета скорректированного коэффициента детерминации выглядит следующим образом: R^2_adj = 1 - (1 - R^2) * (n - 1) / (n - k - 1), где R^2 - обычный коэффициент детерминации, n - количество наблюдений, k - количество предикторов. После подсчета этого коэффициента можно сравнить его значения для разных моделей и выбрать наиболее подходящую модель с наименьшим числом предикторов и при достаточно высоком значении скорректированного коэффициента детерминации.
Как применяется скорректированный коэффициент детерминации?
Скорректированный коэффициент детерминации используется для определения, насколько хорошо выбранная регрессионная модель объясняет вариацию зависимой переменной. Он позволяет сравнивать модели с разным количеством предикторов и выбирать наиболее подходящую модель. Чем ближе значение скорректированного коэффициента детерминации к единице, тем лучше модель объясняет данные.