В мире данных и аналитики, корреляция является одним из основных понятий, используемых для определения силы и направления взаимосвязи между двумя переменными. Ведь понимание этой взаимосвязи позволяет нам делать предсказания и принимать обоснованные решения на основе фактических данных. Если у вас возникла необходимость вычислить коэффициент корреляции или определить, насколько две переменные взаимосвязаны, то это руководство станет для вас необходимым помощником.
Коэффициент корреляции - это числовое значение, которое указывает на силу и направление взаимосвязи между двумя переменными. Если коэффициент положителен, это означает, что при увеличении одной переменной вторая тоже увеличивается, и наоборот, при уменьшении одной переменной вторая также уменьшается. Если коэффициент отрицателен, это указывает на обратную взаимосвязь: при увеличении одной переменной вторая уменьшается, и наоборот.
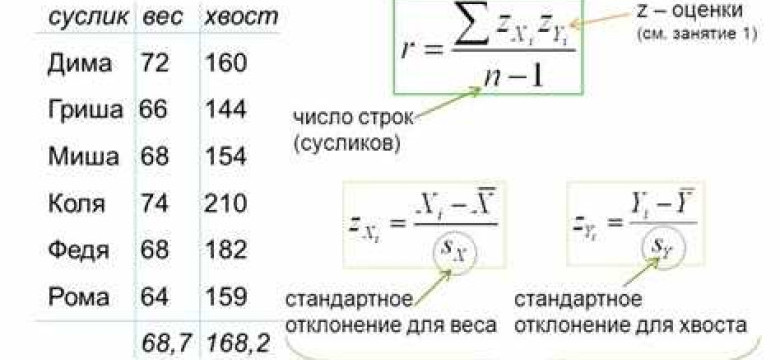
Теперь о том, как найти коэффициент корреляции. Существует несколько методов для вычисления корреляции, но наиболее распространенным является коэффициент корреляции Пирсона. Для его вычисления необходимо знать значения двух переменных для каждого наблюдения. После этого можно воспользоваться формулой для подсчета коэффициента корреляции Пирсона.
Что такое коэффициент корреляции и его значение в статистике
Для найти коэффициент корреляции, необходимо вычислить показатель, который показывает, насколько сильно две переменные взаимосвязаны друг с другом. Это позволяет понять, насколько одна переменная зависит от другой и предсказывать будущие значения на основе имеющихся данных.
Поиск коэффициента корреляции может быть выполнен различными способами, однако наиболее распространенным и удобным методом является использование формулы корреляции Пирсона.
Как определить коэффициент корреляции
- Соберите данные. Для расчета коэффициента корреляции вам понадобятся значения двух переменных, которые вы хотите сравнить. Эти данные могут быть представлены в виде чисел, таблиц или графиков.
- Вычислите средние значения. Для обоих переменных определите их средние значения. Это можно сделать путем сложения всех значений переменной и деления суммы на их количество.
- Вычислите разности. Для каждого значения переменных вычтите среднее значение этой переменной. Это позволит определить разницу между каждым значением переменной и ее средним значением.
- Вычислите произведения. Умножьте соответствующие разности двух переменных. Это позволит определить, насколько каждая пара значений взаимосвязана.
- Вычислите суммы. Просуммируйте все произведения из предыдущего шага. Это позволит получить значение суммы произведений.
- Вычислите квадратные корни. Возьмите квадратный корень из произведения суммы квадратов разностей каждой переменной. Это позволит определить общую изменчивость каждой переменной.
- Вычислите коэффициент корреляции. Разделите значение суммы произведений на произведение квадратных корней, чтобы найти коэффициент корреляции.
Коэффициент корреляции может принимать значение от -1 до 1. Значение, близкое к -1, указывает на обратную (отрицательную) сильную связь между переменными. Значение, близкое к 1, указывает на прямую (положительную) сильную связь между переменными. Значение близкое к 0 указывает на отсутствие связи между переменными.
Как определить коэффициент корреляции между двумя переменными
Поиск и вычисление коэффициента корреляции:
- Соберите данные о двух переменных, которые вы хотите проанализировать. Например, можете взять данные о продажах и рекламных затратах на различные продукты.
- Определите тип корреляции, которую вы хотите вычислить. Существуют различные коэффициенты корреляции, такие как Пирсона, Спирмена и Кендалла. Каждый из них используется в определенных ситуациях и имеет свои особенности.
- Вычислите значение коэффициента корреляции с помощью соответствующей формулы или с использованием специализированного ПО, такого как Excel или статистических пакетов.
- Интерпретируйте полученный результат. Значение коэффициента корреляции близкое к 1 указывает на сильную положительную взаимосвязь, близкое к -1 - на сильную отрицательную взаимосвязь, а близкое к 0 - на отсутствие линейной связи между переменными.
Вычисление и интерпретация коэффициента корреляции позволяют лучше понять взаимосвязь между переменными и помогают принимать правильные решения на основе полученных данных.
Как вычислить коэффициент корреляции вручную
Для определения степени взаимосвязи между двумя переменными мы используем коэффициент корреляции. Коэффициент корреляции позволяет нам измерить, насколько сильно две переменные связаны между собой.
Для вычисления коэффициента корреляции вручную, нужно провести следующие шаги:
- Найти среднее значение (среднюю арифметическую) для каждой из переменных.
- Вычислить отклонение каждого значения переменной от среднего значения этой переменной.
- Умножить отклонение каждого значения первой переменной на отклонение соответствующего значения второй переменной.
- Сложить все полученные произведения.
- Вычислить квадратный корень из произведения суммы отклонений первой переменной умноженной на сумму отклонений второй переменной.
- Разделить полученный результат на n, где n - количество наблюдений.
Итак, формула для вычисления коэффициента корреляции:
| Коэффициент корреляции (r) = | (Σ((X - X̄)(Y - Ӯ))) / (n * σx * σy) |
Где:
- X - значение первой переменной
- Y - значение второй переменной
- X̄ - среднее значение первой переменной
- Ӯ - среднее значение второй переменной
- Σ - сумма
- σx - стандартное отклонение первой переменной
- σy - стандартное отклонение второй переменной
- n - количество наблюдений
Теперь вы знаете, как вычислить коэффициент корреляции вручную. Этот подход позволяет вам лучше понять методологию и улучшить ваше понимание коэффициента корреляции.
Использование статистических программ для расчета коэффициента корреляции

Для определения коэффициента корреляции существуют различные статистические программы, которые позволяют легко и быстро вычислить этот показатель. Такие программы предлагают различные методы расчета коэффициента корреляции, а также позволяют проводить анализ данных, визуализировать результаты и выполнять другие статистические операции.
Как найти коэффициент корреляции в таких программ? Процесс вычисления коэффициента корреляции обычно сводится к нескольким шагам:
- Загрузите в программу данные, для которых необходимо вычислить коэффициент корреляции.
- Выберите соответствующий инструмент или функцию для расчета коэффициента корреляции.
- Укажите переменные, между которыми нужно определить корреляцию.
- Запустите процесс расчета коэффициента корреляции.
- Получите результаты, которые могут быть представлены в виде численного значения коэффициента корреляции и графических диаграмм, отражающих зависимость между переменными.
Следует отметить, что различные статистические программы могут предоставлять разные методы расчета коэффициента корреляции. Например, некоторые программы могут использовать пирсоновский коэффициент корреляции, другие - спирменовский или кендалловский.
Если вы не знакомы с определенной программой, которую хотите использовать для расчета коэффициента корреляции, рекомендуется обратиться к документации или провести поиск информации о расчете коэффициента корреляции в выбранной программе.
Использование статистических программ для расчета коэффициента корреляции значительно упрощает процесс вычисления и позволяет быстро получить результаты. Поэтому, если вам необходимо найти коэффициент корреляции, рекомендуется использовать подходящую статистическую программу для выполнения этой задачи.
| Название программы | Описание | Ссылка |
|---|---|---|
| SPSS | Одна из наиболее популярных программ для статистического анализа данных, включая расчет коэффициента корреляции. | Ссылка |
| R | Бесплатная и открытая система для статистического анализа данных, включая множество пакетов для расчета коэффициента корреляции. | Ссылка |
| Excel | Популярный электронный таблицы с функциями для статистического анализа, включая расчет коэффициента корреляции. | Ссылка |
Расчет коэффициента корреляции в программе [название программы]
Как вычислить коэффициент корреляции?
Для расчета коэффициента корреляции в программе [название программы] необходимо выполнить следующие шаги:
Шаг 1: Откройте программу [название программы] и загрузите данные, для которых нужно найти коэффициент корреляции.
Шаг 2: Определите, какие две переменные в данных вы хотите проанализировать и найти их коэффициент корреляции.
Шаг 3: В программе [название программы] найдите функцию или инструмент для расчета коэффициента корреляции. Это может быть встроенная функция статистического анализа или отдельный модуль.
Шаг 4: Выберите соответствующую переменную и запустите функцию расчета коэффициента корреляции.
Шаг 5: Повторите шаг 4 для каждой пары переменных, для которых нужно вычислить коэффициент корреляции.
Как найти коэффициент корреляции в программе [название программы]?
Для поиска функции расчета коэффициента корреляции в программе [название программы], вы можете использовать поиск внутри программы или обратиться к документации и онлайн руководствам.
В результате выполнения этих шагов, вы сможете определить коэффициент корреляции для выбранных переменных в программе [название программы]. Этот коэффициент будет показателем степени взаимосвязи между этими переменными.
Интерпретация результатов коэффициента корреляции
После вычисления коэффициента корреляции и определения его значения, необходимо понять, как интерпретировать результаты. Коэффициент корреляции позволяет определить насколько сильно связаны две переменные. Значение коэффициента корреляции может изменяться в диапазоне от -1 до 1.
Коэффициент корреляции близкий к -1 означает обратную сильную связь между переменными: чем выше значение одной переменной, тем ниже значение другой. Коэффициент корреляции близкий к 1 означает прямую сильную связь между переменными: чем выше значение одной переменной, тем выше значение другой.
Значение коэффициента корреляции близкое к 0 означает отсутствие линейной связи между переменными. Однако необходимо помнить, что коэффициент корреляции не учитывает возможную нелинейную связь между переменными.
Также важно учитывать, что коэффициент корреляции не является мерой причинно-следственной связи между переменными. Высокий коэффициент корреляции может свидетельствовать о существовании связи между переменными, но не дает информации о том, какая переменная влияет на другую.
Для более точной интерпретации результатов коэффициента корреляции необходимо провести дополнительный анализ и учитывать контекст и особенности исследуемых переменных. Также следует учесть, что значения коэффициента корреляции могут быть подвержены случайным колебаниям, поэтому для получения более достоверных результатов требуется проведение статистической проверки.
Примеры расчета коэффициента корреляции с использованием программы [название программы]
Вычисление коэффициента корреляции может быть сложной задачей, особенно если имеется большой объем данных. В данной статье мы рассмотрим примеры расчета коэффициента корреляции с использованием программы [название программы], которая позволяет определить степень связи между двумя переменными.
Пример 1: Вычисление коэффициента корреляции Пирсона
Допустим, у нас есть две переменные X и Y, и нам необходимо определить коэффициент корреляции между ними. Для этого мы можем воспользоваться программой [название программы], следуя следующим шагам:
- Откройте программу [название программы] и создайте новый проект.
- Импортируйте данные переменных X и Y в программу.
- Выберите функцию для расчета коэффициента корреляции Пирсона.
- Укажите переменные X и Y в качестве входных данных.
- Запустите расчет и дождитесь получения результатов.
- Ознакомьтесь с полученным значением коэффициента корреляции Пирсона.
Таким образом, мы можем использовать программу [название программы], чтобы вычислить коэффициент корреляции Пирсона и определить степень связи между переменными X и Y.
Пример 2: Вычисление коэффициента корреляции Спирмена
Если нам требуется вычислить коэффициент корреляции Спирмена, который измеряет силу монотонной связи между переменными, мы можем использовать программу [название программы] следующим образом:
- Откройте программу [название программы] и загрузите данные переменных X и Y.
- Выберите функцию для вычисления коэффициента корреляции Спирмена.
- Укажите переменные X и Y в качестве входных данных.
- Запустите расчет и дождитесь получения результатов.
- Ознакомьтесь с полученным значением коэффициента корреляции Спирмена.
Таким образом, мы можем использовать программу [название программы], чтобы вычислить коэффициент корреляции Спирмена и определить степень монотонной связи между переменными X и Y.
Поиск коэффициента корреляции: полезные советы и стратегии
Для вычисления коэффициента корреляции важно знать, как определить связь между двумя переменными. Корреляция это статистическая мера, которая позволяет определить степень связи между данными и предсказать их поведение.
Если вы хотите найти коэффициент корреляции, следуйте этим полезным советам и стратегиям:
- Подготовьте данные для анализа, убедитесь, что они числовые.
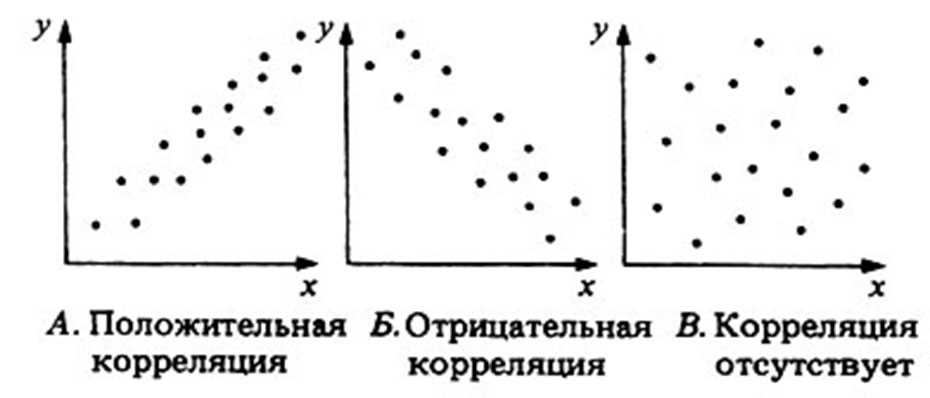
- Определите тип связи между переменными: прямую (положительную) или обратную (отрицательную).
- Воспользуйтесь формулой для вычисления коэффициента корреляции, такой как коэффициент Пирсона.
- Установите значения для каждой переменной и рассчитайте сумму произведений этих значений.
- Вычислите квадратные корни для каждой переменной и перемножьте их.
- Разделите сумму произведений на произведение квадратных корней, чтобы получить коэффициент корреляции.
Заметьте, что коэффициент корреляции всегда находится в диапазоне от -1 до 1. Близкие к 0 значения указывают на отсутствие зависимости, а значения близкие к -1 или 1 указывают на сильную связь между переменными.
Используя эти советы и стратегии, вы сможете определить коэффициент корреляции и понять связь между двумя переменными. Удачного поиска и анализа корреляции!
Видео:
Коэффициент корреляции Пирсона, 2 способа вычисления
Коэффициент корреляции Пирсона, 2 способа вычисления by Аграрёк 15,862 views 3 years ago 5 minutes, 18 seconds
Вопрос-ответ:
Как найти коэффициент корреляции?
Для расчета коэффициента корреляции необходимо следовать определенным шагам. Во-первых, определите набор данных, включающий две переменные. Во-вторых, вычислите среднее значение каждой переменной. Затем вычислите ковариацию между этими переменными, используя формулу. Наконец, разделите полученное значение ковариации на произведение стандартных отклонений каждой переменной, чтобы получить коэффициент корреляции.
Как вычислить коэффициент корреляции?
Для вычисления коэффициента корреляции можно воспользоваться формулой Пирсона. Сначала найдите ковариацию между двумя переменными. Затем вычислите стандартное отклонение каждой переменной. Наконец, поделите ковариацию на произведение стандартных отклонений, чтобы получить коэффициент корреляции. Результат будет находиться в диапазоне от -1 до 1, где 0 означает отсутствие корреляции, а значения -1 или 1 указывают на полную обратную или прямую корреляцию соответственно.
Как определить коэффициент корреляции?
Для определения коэффициента корреляции между двумя переменными можно воспользоваться формулой Пирсона. Необходимо вычислить ковариацию между этими переменными и стандартное отклонение каждой из них. Затем поделить ковариацию на произведение стандартных отклонений. Результат будет являться коэффициентом корреляции, который может принимать значения от -1 до 1. Значение 0 указывает на отсутствие корреляции, а значения -1 и 1 означают полную обратную или прямую корреляцию соответственно.