Стандартная ошибка среднего - это показатель, который позволяет оценить точность оценки средней на основе выборки. Иными словами, это ошибка, которая обычно возникает при использовании среднего значения небольших выборок для прогнозирования среднего значения во всей генеральной совокупности. Другими словами, стандартная ошибка среднего позволяет оценить, насколько близко выборочное среднее значение к истинному среднему значению генеральной совокупности.
Стандартная ошибка среднего является важным инструментом в статистике и имеет решающее значение при обработке данных и проведении исследований. Это помогает исследователям определить, насколько значимыми являются полученные результаты и насколько они можно обобщить на всю генеральную совокупность. Анализировать стандартную ошибку среднего позволяет избежать ошибок в интерпретации и принятии неверных решений на основе выборочных данных.
Как измерить стандартную ошибку среднего?Чтобы измерить стандартную ошибку среднего, необходимо знать не только значения выборки, но и их разброс. Посчитать стандартную ошибку среднего можно с помощью формулы, основанной на стандартном отклонении выборки. Эта формула позволяет определить точность оценки среднего значения на основе имеющихся данных и дает представление о том, насколько ошибка может быть велика.Чем больше выборка, тем меньше стандартная ошибка среднего, потому что с увеличением числа наблюдений точность оценки увеличивается.
Стандартная ошибка среднего: что это такое, как избегать и как измерять
Оценка среднего значения популяции по выборке является статистической оценкой, и ошибка среднего дает нам представление о том, насколько точной может быть эта оценка. Чем меньше стандартная ошибка среднего, тем более точной является наша оценка.
Существует несколько способов избежать стандартной ошибки среднего. Во-первых, можно увеличить объем выборки. Чем больше объектов в выборке, тем более точной будет наша оценка среднего значения.
Во-вторых, можно использовать стратифицированную выборку. Это означает, что мы разделяем генеральную совокупность на более мелкие группы (страты) и затем случайным образом выбираем объекты из каждой страты. Этот подход позволяет учесть разнообразие в генеральной совокупности и уменьшить стандартную ошибку среднего.
Для измерения стандартной ошибки среднего мы используем стандартное отклонение выборки и объем выборки. Формула для расчета стандартной ошибки среднего выглядит следующим образом:
стандартная ошибка среднего = стандартное отклонение выборки / квадратный корень из объема выборки
Измерение стандартной ошибки среднего позволяет нам контролировать точность наших оценок и сделать более точные выводы о генеральной совокупности на основе выборки.
Стандартная средняя ошибка
Средняя ошибка - это мера разброса или стандартное отклонение выборки от среднего значения генеральной совокупности. Она позволяет оценить, насколько среднее значение выборки может отличаться от среднего значения генеральной совокупности.
Стандартная ошибка может быть вычислена по формуле:
| Стандартная ошибка среднего (SE) = | Стандартное отклонение выборки (s) | / | Квадратный корень из размера выборки (n) |
Стандартная ошибка среднего часто используется для проведения статистических тестов и интервальных оценок. Чем меньше стандартная ошибка среднего, тем более точная будет оценка среднего значения генеральной совокупности.
Чтобы избежать или уменьшить стандартную ошибку среднего, необходимо увеличить размер выборки. Чем больше элементов в выборке, тем более точная будет оценка среднего значения генеральной совокупности и, соответственно, меньше стандартная ошибка среднего.
Стандартная ошибка выборки
Стандартная ошибка выборки является оценкой статистической ошибки, которая возникает при оценке среднего значения выборки. Она представляет собой стандартное отклонение средних значений выборок относительно истинного среднего значения выборки.
Определение стандартной ошибки выборки позволяет оценить точность оценки среднего значения выборки и дать представление о том, насколько сильно среднее значение выборки может отличаться от истинного значения.
Избежать стандартной ошибки выборки можно путем достаточного увеличения объема выборки. Чем больше объектов или наблюдений содержит выборка, тем меньше вероятность возникновения стандартной ошибки выборки.
Стандартная ошибка выборки может быть измерена с помощью различных статистических методов. Например, можно использовать стандартное отклонение выборки и объем выборки для расчета стандартной ошибки выборки.
Таким образом, стандартная ошибка выборки является важной характеристикой, которая помогает оценить точность и надежность среднего значения выборки. Избежать этой ошибки можно путем использования достаточно больших объемов выборок. При анализе данных необходимо учитывать стандартную ошибку выборки, чтобы сделать правильные выводы и обеспечить надежные результаты исследования.
Ошибка стандартная
Выборка представляет собой часть генеральной совокупности, из которой были взяты случайные наблюдения. Средняя ошибка стандартная позволяет измерить, насколько среднее значение выборки отличается от среднего значения генеральной совокупности. Чем больше выборка и меньше стандартная ошибка среднего, тем более надежно можно сделать выводы о генеральной совокупности на основе этой выборки.
Ошибка стандартная рассчитывается путем деления стандартного отклонения выборки на квадратный корень из размера выборки. Это позволяет учесть изменчивость данных и размер выборки при оценке ошибки.
Избегать ошибки среднего можно путем увеличения размера выборки. Чем больше выборка, тем более точно можно сделать оценку среднего значения генеральной совокупности.
Измерять ошибку среднего можно с помощью расчета стандартной ошибки или доверительного интервала. Стандартная ошибка среднего показывает разброс средних значений, которые можно ожидать при повторных выборках из генеральной совокупности. Доверительный интервал, в свою очередь, показывает диапазон значений, в котором с определенной вероятностью может находиться среднее значение генеральной совокупности.
Программы
Программы, предназначенные для работы с выборками и оценкой стандартной ошибки средней, позволяют удобно проводить статистический анализ и получать достоверные результаты. Такие программы позволяют рассчитывать стандартную ошибку на основе имеющихся данных и учитывать полное распределение значений в выборке.
Одним из популярных программных решений для работы с выборками данных и оценкой стандартной ошибки средней является программный пакет R. В нем существуют специальные функции для расчета стандартной ошибки и проведения соответствующего статистического анализа. R позволяет рассчитывать различные характеристики выборки, включая среднее значение, стандартное отклонение, стандартную ошибку и другие. Также в R доступна возможность проверять статистические гипотезы и строить графики для визуализации данных.
Другой популярной программой для работы с выборками данных является Microsoft Excel. С помощью функций этой программы также можно рассчитать среднее значение и стандартное отклонение выборки, а также оценить стандартную ошибку средней. В Excel есть специальные функции для работы со статистическими данными, которые позволяют удобно анализировать выборку и получать показатели оценки ошибок.
Программы, предназначенные для работы с выборками данных, помогают исследователям и аналитикам проводить качественный статистический анализ и получать достоверные результаты. Они учитывают стандартные ошибки и позволяют учесть все особенности выборки при оценке среднего значения. Поэтому использование таких программных решений является важным при работе с данными и проведении статистических исследований.
Программное обеспечение для измерения стандартной ошибки среднего
Существует много программных инструментов, предназначенных для измерения стандартной ошибки среднего в выборках. Они позволяют автоматизировать процесс обработки данных и рассчитывать необходимые статистические показатели с высокой точностью.
Программное обеспечение для измерения стандартной ошибки среднего обычно предоставляет следующие возможности:
- Ввод и обработку данных из выборки;
- Расчет среднего значения и стандартного отклонения;
- Вычисление стандартной ошибки среднего;
- Визуализацию результатов, например, в виде графиков или диаграмм;
- Импорт и экспорт данных для дальнейшей анализа.
С использованием такого программного обеспечения становится проще и удобнее проводить статистический анализ данных и получать надежные результаты. Оно помогает исследователям и аналитикам более точно оценить среднее значение выборки и учитывать возможную ошибку в оценке результата.
Важно выбирать программное обеспечение, которое лучше всего соответствует требованиям и задачам исследования. Некоторые из наиболее популярных программ для измерения стандартной ошибки среднего включают в себя SPSS, Excel, R и другие.
Выбор программы зависит от уровня сложности анализа данных, предпочтений пользователя и доступности ресурсов. Независимо от выбора, программное обеспечение для измерения стандартной ошибки среднего помогает улучшить качество статистических измерений и повышает надежность полученных результатов.
Программы для анализа стандартной средней ошибки
Для анализа средней ошибки выборки часто используются специализированные программы, которые облегчают процесс расчетов и предоставляют точные результаты. Вот несколько программ, которые помогут вам в работе с ошибкой средней выборки:
- R: R - это язык программирования и окружение для статистической обработки данных. В R существует много пакетов для работы с стандартной ошибкой средней, например, "standarderror" и "psych". Они предоставляют функции для расчета, визуализации и анализа стандартной ошибки средней выборки.
- SPSS: SPSS - это популярное коммерческое программное обеспечение для статистического анализа данных. В SPSS также есть функции и инструменты для работы с стандартной ошибкой средней выборки. Это мощный инструмент для профессионального анализа данных и создания отчетов.
- Excel: В Microsoft Excel можно использовать стандартные функции, такие как "STDEV" и "STDEVP", для расчета стандартной ошибки средней выборки. Excel также предоставляет возможность создавать графики и диаграммы для визуализации данных.
- Python: Python - это популярный язык программирования, который широко используется для анализа данных. В Python существует множество библиотек, таких как NumPy, SciPy и Pandas, которые содержат функции для расчета стандартной ошибки средней выборки. Они также предоставляют инструменты для визуализации данных и выполнения статистического анализа.
Выбор программы для анализа стандартной ошибки средней выборки зависит от ваших потребностей, уровня опыта и доступного бюджета. Однако, важно помнить, что верное использование программ и правильное интерпретация результатов важны для получения точных и достоверных выводов.
Как избежать стандартной ошибки выборки
1. Размер выборки. Чем больше размер выборки, тем меньше вероятность получения неточной оценки. Поэтому стоит стремиться к использованию как можно большей выборки для улучшения точности и надежности результатов. Например, при проведении опроса выборку следует составлять так, чтобы она была достаточно представительной, то есть включала разнообразные группы людей.
2. Случайность выборки. Чтобы получить более точные результаты, необходимо выбирать образцы случайным образом. Это поможет избежать систематических ошибок и обеспечить представительность выборки.
3. Учет возможных искажений. Во время проведения исследования или эксперимента следует учитывать все потенциальные искажения или влияния, которые могут повлиять на результаты и их интерпретацию. Например, если проводится эксперимент с новым лекарством, стоит учитывать возможные побочные эффекты или внешние факторы, которые могут влиять на эффективность лекарства.
Избегая этих ошибок и принимая во внимание указанные факторы, можно снизить шанс получения неточных результатов и повысить степень достоверности выводов на основе выборки.
Программы для избежания ошибок стандартного измерения
1. Программы для оценки стандартной ошибки выборки
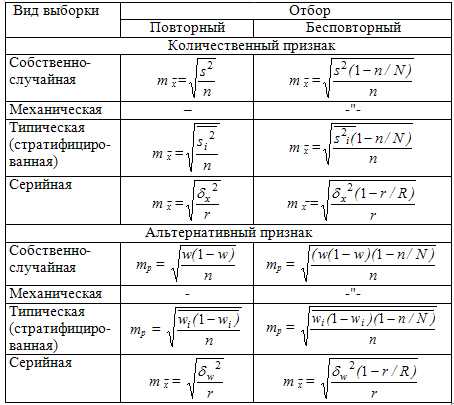
Одной из самых распространенных программ для оценки стандартной ошибки выборки является SPSS (Statistical Package for the Social Sciences). С помощью этой программы можно рассчитать стандартную ошибку выборки и другие статистические показатели на основе данных.
2. Программы для сравнения средних значений выборок
Для сравнения средних значений выборок существуют различные программы, такие как R (язык программирования и среда разработки для статистического анализа), Stata (программа для обработки статистических данных) и Excel (популярная электронная таблица). С их помощью можно проводить сравнительный анализ средних значений выборок и определить стандартную ошибку выборки.
Обратите внимание, что при использовании программ для обработки данных необходимо следить за правильностью исходных данных, а также выбирать подходящие методы анализа. Правильное использование этих программ помогает избежать ошибок стандартного измерения и получить более точные результаты.
Видео:
Открытое собеседование по статистике с Анатолием Карповым | karpov.courses
Открытое собеседование по статистике с Анатолием Карповым | karpov.courses by karpov.courses 24,828 views 1 year ago 1 hour, 37 minutes
Вопрос-ответ:
Что такое стандартная ошибка среднего?
Стандартная ошибка среднего - это мера разброса средних значений, полученных из разных выборок из одной и той же популяции. Она показывает, насколько средние значения различаются от среднего значения в популяции в целом. Большая стандартная ошибка среднего говорит о том, что средние значения в выборках отклоняются от истинного значения в популяции, в то время как маленькая стандартная ошибка среднего указывает на более точные оценки среднего значения.
Как избегать стандартной ошибки среднего?
Избежать стандартной ошибки среднего невозможно, так как она является неизбежной частью процесса выборки. Однако можно уменьшить ее значение, увеличивая объем выборки. Применение строгих критериев исключения выбросов, а также реплицирование эксперимента в разных условиях также может помочь уменьшить стандартную ошибку среднего.
Как измеряется стандартная ошибка среднего?
Стандартная ошибка среднего измеряется в тех же единицах, что и среднее значение, из которого она была получена. Для ее вычисления используется формула, включающая стандартное отклонение и объем выборки. Чем больше выборка, тем меньше стандартная ошибка среднего.