Округление чисел – это процесс приведения числовых значений к более аккуратным и удобным для восприятия цифрам. Оно широко применяется в программировании, финансовых расчетах, статистике и других областях, где точность и правильность цифр имеют особое значение.
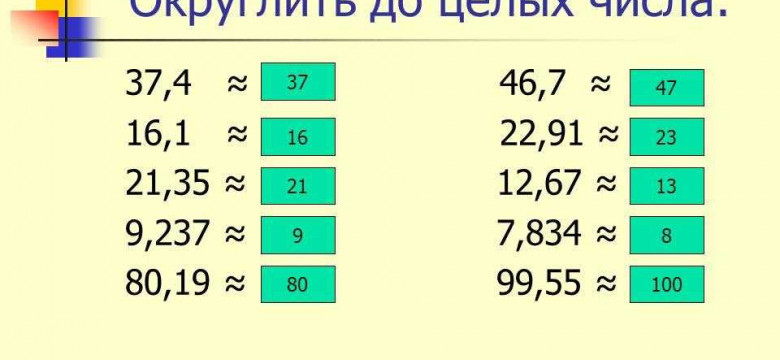
Округление чисел осуществляется в соответствии с определенными правилами. Во-первых, для округления необходимо знать, до какого значения следует округлять. Например, можно округлить число до ближайшей целой цифры, до десятых, сотых и т. д. Во-вторых, правило заключается в том, что если цифра, которая должна быть округлена, меньше пяти, то число округляется вниз, а если цифра больше или равна пяти, то число округляется вверх.
Существует несколько способов округления чисел. Например, можно использовать специальные математические формулы и функции, которые позволяют округлять числа с разной точностью. Также можно использовать условные операторы и циклы, чтобы проверять число на соответствие правилам округления и применять соответствующее изменение.
Аккуратное округление чисел – важный аспект при работе с числовыми значениями. Оно позволяет сохранять нужную точность и предотвращать ошибки в расчетах. Правильное округление чисел – это один из ключевых навыков для программистов и специалистов в других областях, где требуется работа с числами и их значениями.
Округление цифр
Округление чисел основано на применении определенных правил округления, которые определяют, как должны быть округлены цифры в зависимости от их значения. Существуют различные способы округления чисел, включая округление до ближайшего целого числа, округление до определенного числа десятков или сотен, а также округление до определенного количества знаков после запятой.
Округление чисел может быть полезным при работе с большими объемами чисел, когда точность до последней цифры не является критически важной. Например, при анализе статистических данных или деловых расчетах аккуратное округление значений может существенно упростить процесс и улучшить понимание числовых результатов.
Округление цифр также может применяться для представления числовых значений более наглядным способом. Например, когда сумма денежных средств округляется до ближайшего доллара или когда доли процента округляются до целого числа для лучшего восприятия.
Таким образом, округление чисел - это важный инструмент, который позволяет сделать числовые значения более понятными, удобными для анализа и более компактными для представления. Он основан на определенных правилах округления и может быть применен к различным типам цифр и чисел, чтобы получить более простые и удобочитаемые результаты.
Методы округления чисел
Аккуратное закругление чисел - один из способов округления чисел, при котором изменение последней цифры осуществляется в зависимости от ее значения. Если эта цифра меньше или равна пяти, она остается без изменений. Если же она больше пяти, она увеличивается на единицу. Это правило применяется как для положительных, так и для отрицательных чисел.
Закругление чисел также может производиться через применение специальных алгоритмов и правил. Например, для полного закругления чисел, если цифра после последнего разряда меньше пяти, эта цифра отбрасывается. Если же цифра равна или больше пяти, она увеличивается на единицу, а все цифры после нее заменяются на нули.
Округление чисел является важным инструментом при работе с числовыми данными. Оно позволяет упростить значения и сделать их более удобными для анализа и представления.
Округление числовых значений в программировании
Аккуратное округление чисел может быть осуществлено с помощью различных правил и способов. Одно из самых распространенных правил - округление до ближайшего целого числа. В этом случае, если десятичная часть числа больше или равна 0.5, число будет округлено вверх, в противном случае - вниз.
Однако, в программировании существуют и другие способы округления чисел, такие как округление вниз (отбрасывание десятичной части), округление вверх (добавление единицы к целой части) и округление к ближайшему четному числу (четность учитывается при округлении).
Округление чисел в языке программирования Java
В языке программирования Java для округления чисел используется класс BigDecimal, который предоставляет возможность точного округления числовых значений с заданным количеством цифр после запятой. Для округления числа можно использовать методы setScale() и roundingMode() класса BigDecimal.
Округление чисел в языке программирования Python
В языке программирования Python для округления чисел можно использовать функцию round(), которая позволяет задать необходимое количество цифр после запятой. Функция round() округляет число до ближайшего целого числа, с учетом правил округления.
| Язык программирования | Метод округления |
|---|---|
| Java | BigDecimal.setScale() |
| Python | round() |
Корректное округление числовых значений позволяет получить более точные результаты и избежать ошибок, связанных с неточным представлением чисел в компьютере. При разработке программ важно учитывать правила и способы округления, чтобы избежать ошибок округления и получить аккуратные числовые значения.
Понятие точности округления чисел
Закругление чисел
Закругление чисел – простое и понятное понятие. Когда мы округляем число, мы округляем его до ближайшего значения, соответствующего определенной точности. Например, если мы округляем число до двух знаков после запятой, то значение будет округлено до ближайшего числа с двумя цифрами после запятой. Если у нас число 3.14159 и мы округляем его до двух знаков после запятой, то получим 3.14.
Значение точности округления числовых значений
Точность округления числовых значений определяется количеством знаков после запятой, до которых мы округляем число. Например, если мы округляем число до одного знака после запятой, то получаем значения, близкие к указанным знакам после запятой. Если у нас число 1.2356789 и мы округляем его до одного знака после запятой, то получим 1.2.
Но следует помнить, что точность округления чиселовых значений не всегда является единственным фактором. В некоторых случаях также важна точность до целого числа, в других – до тысячных долей. Поэтому выбор точности округления зависит от конкретной ситуации и требований к результату.
Способы аккуратного округления чисел
Существует несколько способов округления числовых значений. Все они направлены на получение более точного и аккуратного округления чисел.
Одним из самых популярных способов является аккуратное закругление. Оно заключается в том, что при округлении чисел в первую очередь учитывается последняя цифра, которую нужно округлить.
Для аккуратного округления чисел следует придерживаться следующих правил:
| Если последняя цифра, которую нужно округлить, меньше пяти, то она просто отбрасывается. |
| Если последняя цифра равна пяти, то она округляется вверх, если перед ней стоит нечетное число, и вниз, если перед ней стоит четное число. |
| Если последняя цифра больше пяти, то она округляется вверх. |
Аккуратное округление чисел позволяет получить более точные результаты при вычислениях и представить числа в более читаемом виде.
Округление вещественных чисел
Округление вещественного числа может выполняться по различным правилам, в зависимости от ситуации. Наиболее распространенные правила округления чисел:
1. Округление по математическим правилам
При округлении числа по математическим правилам применяется следующее правило: если десятичная часть числа больше или равна 0.5, то число округляется в большую сторону, иначе число округляется в меньшую сторону. Например, число 3.7 будет округлено до 4, а число 2.3 будет округлено до 2.
2. Округление к ближайшему четному
Округление к ближайшему четному применяется в некоторых областях, чтобы уменьшить случайную погрешность при округлении. При округлении числа к ближайшему четному, число округляется в ту сторону, которая ближе к четному числу. Например, число 3.5 будет округлено до 4, а число 2.5 будет также округлено до 4.
Округление вещественных чисел является важным инструментом при обработке числовых значений. В зависимости от требований и контекста, можно выбирать различные правила округления для достижения наилучшего результата. Необходимо помнить, что округление должно быть аккуратным и учитывать особенности числовых значений, чисел и цифр, с которыми вы работаете.
Плюсы и минусы различных методов округления
1. Метод математического округления
- Округление значений осуществляется к ближайшему целому числу.
- Этот метод является наиболее распространенным и простым.
- Подходит для случаев, когда нужно получить аккуратное округление числа.
- Однако, данный метод может приводить к большим отклонениям при округлении значений, близких к половине.
2. Метод округления вниз (отбрасывание дробной части)
- Округление чисел производится путем отбрасывания дробной части числа.
- Этот метод часто используется для технических расчетов, где нужно получить целое значение для дальнейших операций.
- Округление вниз может приводить к потере точности при округлении значений, близких к положительным целым числам.
3. Метод округления вверх (прибавление единицы)
- Округление чисел осуществляется путем прибавления единицы к дробной части.
- Этот метод используется, когда нужно гарантировать округление чисел в большую сторону.
- Метод округления вверх может приводить к потере точности при округлении значений, близких к отрицательным целым числам.
Выбор метода округления чисел зависит от задачи и требуемой точности. Важно учитывать особенности каждого метода и его влияние на результаты вычислений.
Округление числовых значений с учетом особенностей задачи
Одним из наиболее распространенных правил округления является аккуратное округление до определенного количества цифр после запятой. Например, если требуется закруглить число 3.45678 до двух знаков после запятой, то результатом будет 3.46. В этом случае, если третья цифра после запятой больше или равна 5, то следующая цифра увеличивается на 1 и все последующие цифры обнуляются.
Также округление чисел может быть произведено с учетом значений других чисел. Например, если требуется аккуратно округлить числа в списке суммы до целых чисел, то при округлении каждого числа добавляется сумма округленных предыдущих чисел. Например, если имеется список чисел [1.2, 2.5, 3.8], то аккуратное округление будет выглядеть следующим образом: 1.2 -> 1, 2.5 -> 3 (1 + 2.5 округленное предыдущее число), 3.8 -> 7 (3 + 3.8 округленное предыдущее число).
Таким образом, в каждой задаче следует учитывать особенности округления числовых значений: количество цифр после запятой, наличие других чисел и правила округления. Это поможет получить точные и аккуратно округленные значения чисел, удовлетворяющие требованиям конкретной задачи.
Видео:
Математика 5 класс. Округление чисел
Математика 5 класс. Округление чисел by Ирина Викторовна Васильева 7,973 views 4 years ago 4 minutes, 12 seconds
Вопрос-ответ:
Почему округление чисел важно?
Округление чисел важно, так как оно позволяет упростить и удобно представить большие числовые значения. Также округление используется для выполнения математических операций и сравнений чисел.
Какие существуют правила округления числовых значений?
Существует несколько правил округления чисел: правило "к ближайшему", когда если дробная часть числа больше или равна 0.5, то число округляется в большую сторону, если меньше 0.5 - в меньшую; правило "вниз", когда число всегда округляется в меньшую сторону; правило "вверх", когда число всегда округляется в большую сторону; правило "нули", когда число округляется в меньшую сторону, если дробная часть числа равна 0.5 и округляется к ближайшему четному числу, если дробная часть числа равна 0.5 и число нечетное.
Как округлять цифры чисел?
Для округления цифр чисел используются те же правила, что и для округления чисел в целом. Если цифра больше или равна 5, то она округляется в большую сторону, если меньше 5 - в меньшую сторону. Например, число 3.54 округляется до 3.5, а число 7.96 - до 8.0.
Как проводить аккуратное округление чисел?
Для проведения аккуратного округления чисел нужно следовать определенным правилам. Если дробная часть числа равна 0.5, то число округляется к ближайшему четному числу. Например, число 2.5 округляется до 2, а число 3.5 - до 4.
Какое округление чисел является наиболее распространенным и применяемым?
Наиболее распространенным и применяемым является округление "к ближайшему". Такое округление используется во многих сферах, например, при расчетах с деньгами, физических и химических величинах, при оценке и рейтинге.