Линейная регрессия является одним из наиболее популярных методов анализа данных и прогнозирования. Во многих ситуациях, особенно при работе с большими объемами информации, возникает необходимость в создании модели, которая позволит выделить наиболее существенные факторы и предсказать будущие значения. В этом случае, линейная регрессия в Excel может стать незаменимым инструментом.
Основная идея линейной регрессии заключается в том, чтобы найти наилучшую прямую, которая наиболее точно соответствует зависимости между независимыми и зависимыми переменными. В Excel существует возможность провести как простую линейную регрессию с одной независимой переменной, так и множественную линейную регрессию с несколькими независимыми переменными.
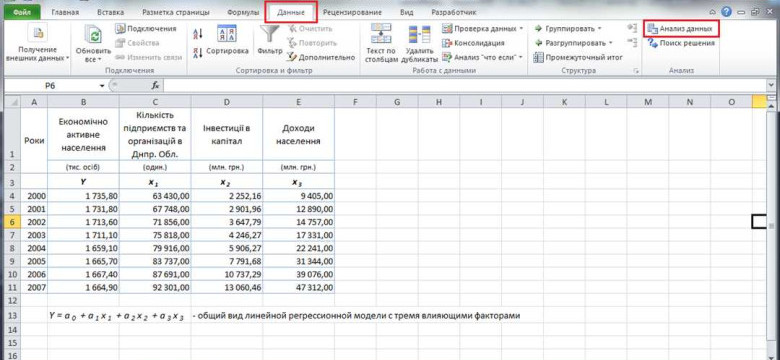
В Excel для проведения линейной регрессии используется функция "Регрессия" в разделе "Анализ данных". При помощи этой функции можно построить модель и получить точные прогнозы на основе имеющихся данных. Результаты анализа представляются в виде графика и таблицы с коэффициентами регрессии, которые позволяют оценить степень влияния каждого из факторов на зависимую переменную.
Линейная регрессия в Excel: проведение анализа и получение прогнозов
Excel предоставляет удобный и простой способ рассчитать линейную регрессию и получить точные прогнозы. Для этого можно использовать функцию "ЛинРег" или инструмент "Анализ данных".
Применение линейной регрессии в Excel
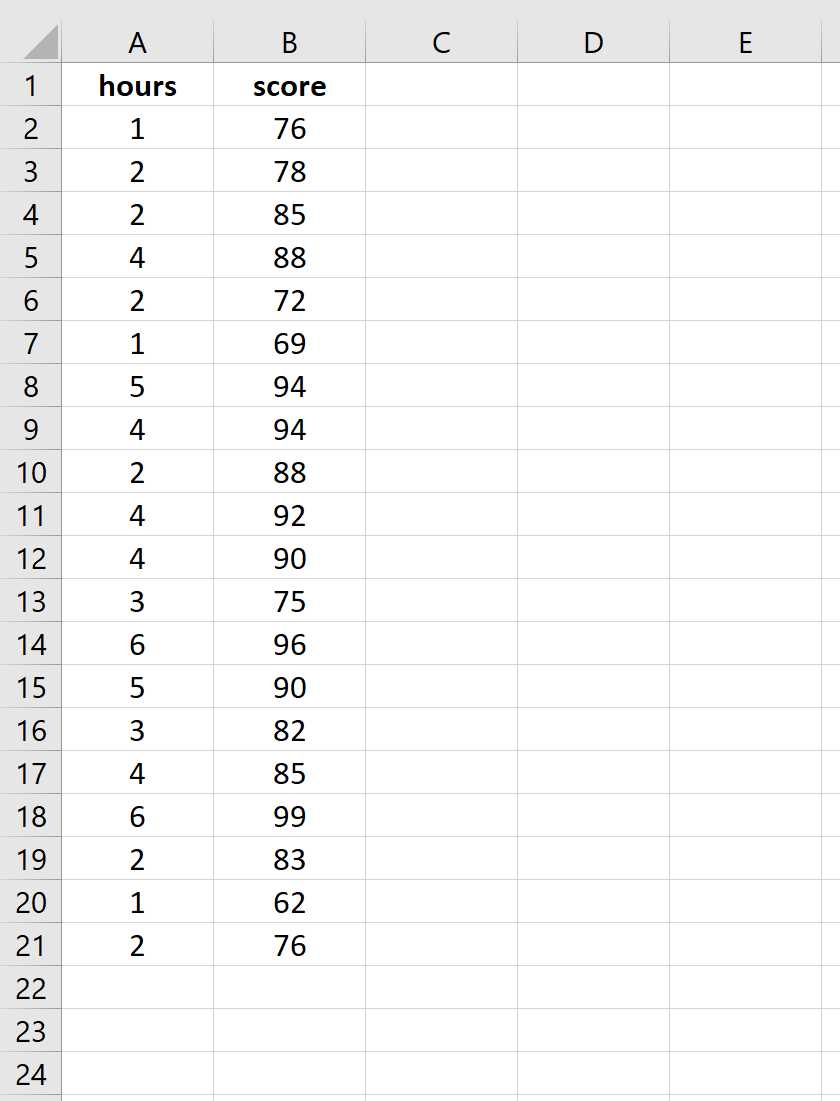
Для проведения линейной регрессии в Excel необходимо иметь данные, включающие зависимую переменную и одну или несколько независимых переменных. В Excel данные обычно представлены в виде таблицы, где каждая строка представляет отдельное наблюдение, а каждый столбец - переменную.
Одним из способов проведения линейной регрессии в Excel является использование функции "ЛинРег". Для этого необходимо выделить ячейки, в которых находятся зависимая и независимые переменные, и ввести формулу "=ЛинРег(зависимая_переменная; независимые_переменные; [константа])". Результатом будет уравнение линейной регрессии, где значения коэффициентов указывают на величину и направление связи между переменными.
Множественная линейная регрессия в Excel
Множественная линейная регрессия используется, когда зависимая переменная связана с несколькими независимыми переменными. В Excel это можно реализовать с помощью функции "ЛинРегМнож". Формула для множественной линейной регрессии выглядит следующим образом: "=ЛинРегМнож(зависимая_переменная; независимые_переменные; [константа])". Результатом будет уравнение множественной линейной регрессии, которое позволяет прогнозировать значения зависимой переменной на основе значений независимых переменных.
Выводы:
Линейная регрессия в Excel предоставляет возможность проведения анализа и получения прогнозов на основе имеющихся данных. Используя функцию "ЛинРег" или "ЛинРегМнож", можно рассчитать уравнение линейной или множественной регрессии, которое позволит определить связь между переменными и сделать точные прогнозы. Это полезный инструмент для анализа данных и принятия решений.
Регрессия в Excel: основные понятия и принципы
В Excel можно проводить как простую линейную регрессию, так и множественную линейную регрессию. Простая линейная регрессия используется, когда есть только одна независимая переменная, в то время как множественная линейная регрессия используется, когда есть две или более независимых переменных.
Для проведения регрессионного анализа в Excel можно воспользоваться функцией "Линейная регрессия" или с помощью инструментов анализа данных. Функция "Линейная регрессия" позволяет получить коэффициенты линейной регрессии, а также прогнозировать значения зависимой переменной на основе известных значений независимых переменных.
При проведении регрессионного анализа в Excel необходимо учитывать следующие принципы:
- Независимые переменные должны быть числовыми и непрерывными.
- Зависимая переменная должна быть числовой и иметь линейную связь с независимыми переменными.
- Данные должны быть представлены в виде таблицы, где каждая строка соответствует наблюдению, а каждый столбец - переменной.
- Должны быть достаточно данных, чтобы можно было провести адекватный анализ.
Проведение регрессионного анализа в Excel позволяет получить точные прогнозы значений зависимой переменной на основе известных значений независимых переменных. Эта информация может быть полезна для прогнозирования будущих тенденций, оптимизации бизнес-процессов и принятия важных решений.
Прогнозирование с помощью регрессии: преимущества и ограничения
Одним из главных преимуществ множественной регрессии в Excel является возможность прогнозирования. На основе полученной модели можно предсказать значения зависимой переменной для новых наблюдений, которые отсутствуют в исходном наборе данных. Это позволяет сделать более точные прогнозы и принять более обоснованные решения в будущем. Прогнозирование с помощью регрессии может быть полезно во многих областях, включая маркетинг, финансы, экономику и науку.
Однако, необходимо отметить и некоторые ограничения модели множественной регрессии в Excel. Во-первых, предпосылка о линейной зависимости между переменными может быть нарушена в случае нелинейных связей. В таких случаях, линейная модель может давать неправильные или неточные прогнозы. Во-вторых, множественная регрессия в Excel чувствительна к выбросам и наличию мультиколлинеарности - высокой корреляции между независимыми переменными. Это может привести к искажению результатов и неправильным выводам.
Тем не менее, с учетом этих ограничений, модель множественной регрессии в Excel остается мощным инструментом для анализа данных и прогнозирования. Правильное использование этой модели может помочь в принятии обоснованных решений, оптимизации бизнес-процессов и достижении успеха в различных областях деятельности.
Множественная регрессия в Excel: анализ влияния нескольких факторов
Excel предоставляет удобные инструменты для проведения анализа множественной регрессии. Для этого необходимо использовать функцию "Линейная регрессия" в Excel, которая позволяет включить несколько независимых переменных в модель регрессии.
Для анализа влияния нескольких факторов при помощи множественной регрессии в Excel необходимо:
- Открыть Excel и создать новую таблицу.
- В первом столбце таблицы ввести значения зависимой переменной.
- В следующих столбцах ввести значения независимых переменных.
- Выбрать данные, которые нужно проанализировать, и нажать на кнопку "Данные" в верхней панели Excel.
- Выбрать функцию "Линейная регрессия" из списка доступных функций.
- Выбрать зависимую переменную и независимые переменные в соответствующих полях.
- Нажать кнопку "ОК" и дождаться результатов анализа множественной регрессии.
После проведения анализа множественной регрессии в Excel вы получите результаты, которые позволят оценить влияние каждой независимой переменной на зависимую переменную. Вы сможете видеть коэффициенты регрессии для каждой независимой переменной, а также общую модель регрессии.
Множественная регрессия в Excel дает возможность получать точные прогнозы, анализировать влияние нескольких факторов на зависимую переменную и строить модели, которые будут более точно учитывать все факторы, влияющие на исследуемый процесс.
Случайные ошибки в линейной регрессии: как с ними работать
В линейной регрессии в Excel случайные ошибки могут возникать из-за различных факторов, таких как недостаточное количество данных, наличие выбросов или некорректная спецификация модели. Случайные ошибки представляют собой расхождение между фактическими наблюдениями и значениями, предсказанными моделью.
Для работы с случайными ошибками в линейной регрессии в Excel, важно оценить их характер и их влияние на результаты модели. Одним из стандартных способов оценки случайных ошибок является анализ остатков. Остатки в линейной регрессии представляют собой разницу между фактическими значениями зависимой переменной и значениями, предсказанными моделью.
Для анализа остатков в Excel можно построить график остатков по прогнозным значениям. Если остатки случайным образом распределены вокруг нуля и не имеют явной структуры, это может говорить о том, что модель хорошо объясняет данные и случайные ошибки несущественны.
Однако, если график остатков показывает некоторую систематичность или наличие неслучайных закономерностей, это может указывать на проблемы в модели. Например, остатки могут быть неравномерно распределены вокруг нуля или иметь тренд. В таком случае, возможно потребуется изменение модели или учет дополнительных факторов.
Еще одной полезной метрикой для оценки случайных ошибок в линейной регрессии в Excel является коэффициент детерминации (R-квадрат). R-квадрат показывает, насколько хорошо модель объясняет изменчивость зависимой переменной. Если R-квадрат близок к единице, это указывает на то, что модель достаточно точно предсказывает значения зависимой переменной и случайные ошибки вносят незначительный вклад.
В целом, работа с случайными ошибками в линейной регрессии в Excel требует внимательного анализа остатков и оценки их влияния на результаты модели. Если ошибки незначительны или несистематичны, а показатели модели (например, R-квадрат) высоки, это указывает на хорошую точность и достоверность модели. Однако, если остатки имеют систематичность или значительный вклад, возможно потребуется корректировка модели или учет дополнительных факторов для более точных прогнозов.
Линейная модель в Excel: использование и интерпретация результатов
Линейная регрессия в Excel позволяет строить множественную линейную модель, которая помогает анализировать и прогнозировать взаимосвязи между переменными. Для проведения анализа и интерпретации результатов линейной модели в Excel необходимо собрать данные, определить зависимую переменную и факторы, выбрать алгоритм и построить модель.
Excel предоставляет удобный инструмент для проведения линейной регрессии. Для этого необходимо выбрать столбцы с данными, затем воспользоваться функцией "Регрессия" в разделе "Анализ данных". После этого Excel выдаст результаты регрессионного анализа, включающие коэффициенты регрессии, стандартные ошибки, значимость коэффициентов, а также статистические метрики качества модели.
Интерпретация результатов линейной модели основывается на значении коэффициентов регрессии. Коэффициенты отражают взаимосвязь между зависимой переменной и факторами. Например, положительный коэффициент означает, что увеличение значения фактора ведет к увеличению зависимой переменной. Отрицательный коэффициент указывает на противоположную связь между переменными.
Стандартные ошибки коэффициентов позволяют оценить точность оценок коэффициентов. Низкие стандартные ошибки говорят о более точных оценках коэффициентов, что делает их статистически значимыми.
Для оценки качества модели в Excel используются различные статистические метрики, такие как коэффициент детерминации R^2 и F-статистика. Коэффициент детерминации показывает, насколько хорошо модель объясняет изменение зависимой переменной. F-статистика позволяет оценить общую значимость модели.
Использование и интерпретация результатов линейной модели в Excel позволяют получать точные прогнозы и анализировать взаимосвязи между переменными. Это полезный инструмент для исследователей, аналитиков и всех, кто работает с данными и стремится улучшить прогнозирование и принятие решений.
Способы улучшения точности прогнозов в линейной регрессии
Линейная регрессия в Excel предоставляет мощный инструмент для анализа и прогнозирования данных. Однако, чтобы получить более точные прогнозы, можно применить несколько способов улучшения модели.
Во-первых, можно использовать множественную регрессию в Excel. Множественная регрессия позволяет учитывать несколько независимых переменных, что может повысить точность модели. В Excel это можно сделать, указав несколько столбцов с данными в качестве независимых переменных при построении регрессионной модели.
Во-вторых, можно провести анализ выбросов и исключить их из данных. Выбросы могут искажать результаты линейной регрессии и приводить к неточным прогнозам. В Excel можно визуализировать данные на графике рассеяния и идентифицировать выбросы. После этого их можно удалить из данных или применить методы робастной регрессии.
Также можно применить методы предварительной обработки данных, такие как стандартизация или нормализация, чтобы устранить возможные проблемы с масштабированием данных и улучшить точность регрессионной модели в Excel.
Еще один способ улучшения точности прогнозов - это включение в модель дополнительных полиномиальных или взаимодействующих переменных. Это может помочь учесть нелинейные зависимости и взаимодействия между переменными, что улучшит точность прогнозов линейной регрессии в Excel.
В целом, применение этих способов исследования и улучшения модели линейной регрессии в Excel позволяет создать более точные прогнозы и получить более полное представление о зависимостях между переменными.
Оценка качества модели линейной регрессии в Excel
Коэффициент детерминации может принимать значение от 0 до 1, где 1 означает идеальную соответствие модели данным, а 0 означает полное отсутствие связи между переменными. Чем ближе значение R-квадрат к единице, тем лучше модель соответствует данным.
В Excel R-квадрат можно вычислить с помощью функции RSQ. Для этого необходимо выбрать область значений прогнозируемых и фактических данных, а затем ввести формулу: =RSQ(y-значения; x-значения).
Кроме коэффициента детерминации, также полезно оценивать стандартную ошибку регрессии (SER), которая показывает разброс фактических значений относительно линии регрессии. Чем меньше SER, тем точнее модель предсказывает данные.
В Excel SER можно вычислить с помощью функции STEYX. Для этого также необходимо выбрать область значений прогнозируемых и фактических данных, а затем ввести формулу: =STEYX(y-значения; x-значения).
Кроме этих основных показателей, в Excel также есть возможность оценки значимости коэффициентов регрессии с помощью t-теста и анализа значимости модели в целом с помощью F-теста.
Метод множественной регрессии в Excel позволяет оценить значительное количество переменных одновременно и определить их влияние на зависимую переменную. Это позволяет получить более точные и обоснованные прогнозы в сравнении с простой линейной регрессией.
Альтернативные методы анализа и прогнозирования в Excel
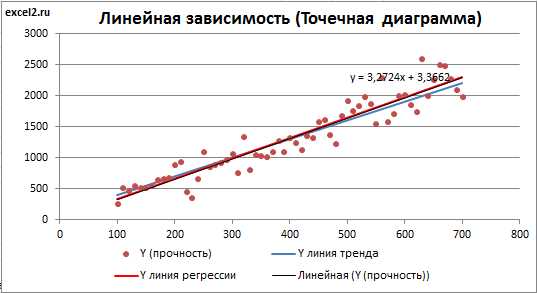
Чтобы провести множественный анализ, необходимо собрать данные о нескольких независимых переменных и зависимую переменную. Затем, используя инструменты анализа данных в Excel, можно построить множественную модель линейной регрессии и получить точные прогнозы.
Множественная регрессия в Excel позволяет учесть влияние различных факторов на исследуемую зависимую переменную. Это особенно полезно в ситуациях, когда одна независимая переменная не может полностью объяснить изменения зависимой переменной. В модели множественной регрессии можно учесть несколько факторов одновременно, что позволяет получить более точные прогнозы и более полное понимание влияния различных факторов на исследуемую переменную.
Шаги по проведению множественного анализа в Excel:
- Соберите данные о нескольких независимых переменных и зависимой переменной.
- Откройте Excel и выберите нужную таблицу с данными.
- На вкладке «Данные» найдите раздел «Анализ» и выберите «Множественная линейная регрессия».
- В появившемся диалоговом окне укажите диапазоны для зависимой и независимых переменных.
- Нажмите «ОК» и дождитесь завершения анализа.
- Получите результаты анализа, включая коэффициенты регрессии, значимость модели и точность прогнозов.
Множественная регрессия в Excel – это мощный инструмент анализа данных, который позволяет получить более точные прогнозы и более глубокое понимание влияния различных факторов на зависимую переменную. Используя множественную модель линейной регрессии, можно сделать более обоснованные решения и прогнозы, основанные на количественных анализах данных.
Видео:
Ограничивающие убеждения, тема: деньги
Ограничивающие убеждения, тема: деньги by Александр Герасимов НЛП 236 views Streamed 7 hours ago 1 hour, 1 minute
Вопрос-ответ:
Как провести анализ и получить точные прогнозы с помощью линейной регрессии в Excel?
Для проведения анализа и получения точных прогнозов с помощью линейной регрессии в Excel, вам необходимо сначала импортировать свои данные в программу. Затем выберите данные и откройте вкладку "Вставка" в верхней части окна программы. В группе "Таблицы" выберите "Диаграмма рассеяния". Выберите тип диаграммы рассеяния и постройте график на основе выбранных данных. Затем перейдите на вкладку "Анализ данных" и выберите "Регрессия". Введите входные данные и настройки регрессии, а затем нажмите "ОК". Excel выполнит анализ регрессии и предоставит вам точные прогнозы, основанные на введенных данных.
Как провести множественную регрессию в Excel?
Чтобы провести множественную регрессию в Excel, вы можете использовать функцию "Регрессия" из пакета анализа данных. Для начала, выберите ваши входные данные и откройте вкладку "Анализ данных" в верхней части окна программы. Найдите и выберите функцию "Регрессия" в списке доступных аналитических инструментов. Введите входные данные и настройки регрессии, такие как диапазон явных переменных и диапазон зависимых переменных. Затем нажмите "ОК", и Excel выполнит анализ множественной регрессии на основе введенных данных.
Какая разница между линейной моделью и линейной регрессией в Excel?
Линейная модель и линейная регрессия в Excel являются связанными понятиями, но имеют некоторые различия. Линейная модель - это математическая модель, которая описывает линейную зависимость между входными переменными и выходной переменной. Линейная регрессия, с другой стороны, является статистическим методом, который используется для оценки и анализа линейной модели. В Excel, линейная регрессия предоставляет специальные инструменты и функции для анализа линейных моделей и получения точных прогнозов на основе введенных данных.